题目内容
函数f(x)=ax2+x-1+3a(a∈R)在区间[-1,1]上有零点,求实数a的取值范围.
考点:函数的零点
专题:函数的性质及应用
分析:当a=0时,f(x)=x-1满足条件;当a≠0时,函数f(x)在区间[-1,1]上有零点分为三种情况:①方程f(x)=0在区间[-1,1]上有重根,②若函数y=f(x)在区间[-1,1]上只有一个零点,但不是f(x)=0的重根,③若函数y=f(x)在区间[-1,1]上有两个零点,分类讨论求出满足条件的a的范围后,综合讨论结果,可得答案.
解答:
解:当a=0时,f(x)=x-1,令f(x)=0,得x=1,是区间[-1,1]上的零点.
当a≠0时,函数f(x)在区间[-1,1]上有零点分为三种情况:
①方程f(x)=0在区间[-1,1]上有重根,
令△=1-4a(-1+3a)=0,解得a=-
或a=
.
当a=-
时,令f(x)=0,得x=3,不是区间[-1,1]上的零点.
当a=
时,令f(x)=0,得x=-1,是区间[-1,1]上的零点.
②若函数y=f(x)在区间[-1,1]上只有一个零点,但不是f(x)=0的重根,
令f(1)f(-1)=4a(4a-2)≤0,解得0<a≤
.
③若函数y=f(x)在区间[-1,1]上有两个零点,
则
或
解得a∈∅.
综上可知,实数a的取值范围为[0,
].
当a≠0时,函数f(x)在区间[-1,1]上有零点分为三种情况:
①方程f(x)=0在区间[-1,1]上有重根,
令△=1-4a(-1+3a)=0,解得a=-
| 1 |
| 6 |
| 1 |
| 2 |
当a=-
| 1 |
| 6 |
当a=
| 1 |
| 2 |
②若函数y=f(x)在区间[-1,1]上只有一个零点,但不是f(x)=0的重根,
令f(1)f(-1)=4a(4a-2)≤0,解得0<a≤
| 1 |
| 2 |
③若函数y=f(x)在区间[-1,1]上有两个零点,
则
|
|
解得a∈∅.
综上可知,实数a的取值范围为[0,
| 1 |
| 2 |
点评:本题考查二次函数与方程之间的关系,二次函数在给定区间上的零点问题,要注意函数图象与x轴相切的情况,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
| ∫ | 2 1 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x3 |
A、ln 2+
| ||
B、ln 2-
| ||
C、ln 2-
| ||
D、ln 2-
|
点A(2,0),B(4,2),若|
|=2|
|,则点C坐标为( )
| AB |
| AC |
| A、(1,-1) |
| B、(1,-1)或(5,-1) |
| C、(1,-1)或(3,1) |
| D、无数多个 |
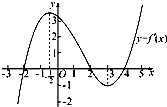 如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数的图象如图所示,给出下列判断: