题目内容
1．已知f（x）=$\left\{\begin{array}{l}{x^3}，x≥0\\|lg（-x）|，x＜0\end{array}$，则函数y=2f2（x）-3f（x）的零点个数为5．分析 令y=2f2（x）-3f（x）=0，则f（x）=0，或f（x）=$\frac{3}{2}$，画出函数f（x）=$\left\{\begin{array}{l}{x^3}，x≥0\\|lg（-x）|，x＜0\end{array}$的图象，可得答案．
解答 解：令y=2f2（x）-3f（x）=0，
则f（x）=0，或f（x）=$\frac{3}{2}$，
函数f（x）=$\left\{\begin{array}{l}{x^3}，x≥0\\|lg（-x）|，x＜0\end{array}$的图象如下图所示：
由图可得：f（x）=0有2个根，或f（x）=$\frac{3}{2}$有3个根，
故函数y=2f2（x）-3f（x）的零点个数为5个，
故答案为：5
点评 本题考查的知识点是函数的零点，数形结合思想，分段函数的应用，难度中档．
练习册系列答案
阅读快车系列答案
相关题目
如图，在三棱柱ABC-A1B1C1中，AB⊥BC，AB1⊥平面ABC，且AB=BC=AB1=2．
9．已知$cos（\frac{3π}{14}-θ）=\frac{1}{3}$，则$sin（\frac{2π}{7}+θ）$=（ ）
| A． | $\frac{1}{3}$ | B． | $-\frac{1}{3}$ | C． | $\frac{{2\sqrt{2}}}{3}$ | D． | $-\frac{{2\sqrt{2}}}{3}$ |
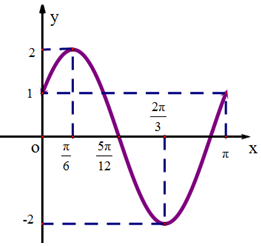已知函数$f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜\frac{π}{2}）$的部分图象如图所示．