题目内容
11. 如图,在三棱柱ABC-A1B1C1中,AB⊥BC,AB1⊥平面ABC,且AB=BC=AB1=2.
如图,在三棱柱ABC-A1B1C1中,AB⊥BC,AB1⊥平面ABC,且AB=BC=AB1=2.(Ⅰ)证明:平面C1CBB1⊥平面A1ABB1
(Ⅱ)若点P为A1C1的中点,求直线BP与平面A1ACC1所成角的正弦值.
分析 (Ⅰ)B1A⊥平面ABC,则B1A⊥BC,AB⊥BC,BC⊥平面A1ABB1,BC?平面C1CBB1,平面C1CBB1⊥平面A1ABB1;
(Ⅱ)分别以$\overrightarrow{BC},\overrightarrow{BA},\overrightarrow{BM}$为x,y,z轴的非负向量建立空间直角坐标系B-xyz,求得$\overrightarrow{BP}$=(1,3,2)和平面A1ACC1法向量,直线BP与平面A1ACC1所成角的余弦值为丨cos<$\overrightarrow{n}$,$\overrightarrow{BP}$>丨=丨$\frac{1+3-2}{\sqrt{3}×\sqrt{14}}$丨=$\frac{\sqrt{42}}{21}$,根据同角三角形函数的基本关系,即可求得直线BP与平面A1ACC1所成角的正弦值.
解答 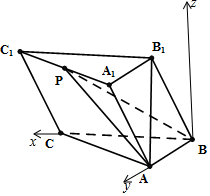 解:(Ⅰ)证明:∵B1A⊥平面ABC,
解:(Ⅰ)证明:∵B1A⊥平面ABC,
∴B1A⊥BC…(1分),
又∵AB⊥BC,AB∩BC=B,
∴BC⊥平面A1ABB1,…(3分),
又∵BC?平面C1CBB1,
∴平面C1CBB1⊥平面A1ABB1…(4分)
(Ⅱ)过B点作BM⊥平面ABC,则BM⊥BA,BM⊥BC,分别以$\overrightarrow{BC},\overrightarrow{BA},\overrightarrow{BM}$为x,y,z轴的非负向量建立空间直角坐标系B-xyz,…(5分),
则B(0,0,0),B1(0,2,2),
∵$\overrightarrow{A{A}_{1}}$=$\overrightarrow{B{B}_{1}}$=$\overrightarrow{C{C}_{1}}$=(0,2,2),
∴A1(0,4,2),C1(2,2,2),P(1,3,2),
∴$\overrightarrow{AC}$=(2,-2,0),$\overrightarrow{BP}$=(1,3,2),
设$\overrightarrow{n}$=(x,y,z)为平面A1ACC1的一个法向量,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=0}\\{\overrightarrow{n}•\overrightarrow{A{A}_{1}}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2x-2y=0}\\{2y+2z=0}\end{array}\right.$,取x=1,解得:y=1,z=-1,
∴$\overrightarrow{n}$=(1,1,-1),
故直线BP与平面A1ACC1所成角的余弦值为丨cos<$\overrightarrow{n}$,$\overrightarrow{BP}$>丨=丨$\frac{1+3-2}{\sqrt{3}×\sqrt{14}}$丨=$\frac{\sqrt{42}}{21}$,
sin<$\overrightarrow{n}$,$\overrightarrow{BP}$>=$\sqrt{1-(\frac{\sqrt{42}}{21})^{2}}$=$\frac{\sqrt{399}}{21}$.…(12分)
点评 本题考查的知识点是用空间向量求直线与平面的夹角,考查立体几何与向量的综合应用,考查平面法向量的求法,考查计算能力,属于中档题.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 如图为平面中两个全等的直角三角形,将这两个三角形绕着它们的对称轴(虚线所在直线)旋转一周得到一个几何体,则该几何体的体积为( )
如图为平面中两个全等的直角三角形,将这两个三角形绕着它们的对称轴(虚线所在直线)旋转一周得到一个几何体,则该几何体的体积为( )| A. | 4π | B. | 8π | C. | 16π | D. | 32π |