题目内容
函数y=(m2-m-1)xm2-2m-2是幂函数，且在x∈（0，+∞）上为增函数，则实数m的值为 ．
考点：幂函数的单调性、奇偶性及其应用
专题：函数的性质及应用
分析：根据幂函数的定义和性质建立条件关系即可得到结论．
解答：
解：∵函数y=(m2-m-1)xm2-2m-2是幂函数，
∴m2-m-1=1，解得m=2或m=-1，
又∵函数在x∈（0，+∞）上为增函数，
∴m2-2m-2＞0，故m=-1．
故答案为：-1
∴m2-m-1=1，解得m=2或m=-1，
又∵函数在x∈（0，+∞）上为增函数，
∴m2-2m-2＞0，故m=-1．
故答案为：-1
点评：本题考查了幂函数的概念及性质，注意幂函数的系数为1，比较基础．
练习册系列答案
相关题目
四棱锥S-ABCD，底面ABCD为平行四边形，侧面SBC⊥底面ABCD．已知∠DAB=135°，BC=2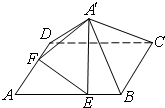
如图，已知正方形ABCD的边长为6，点E，F分别在边AB，AD上，AE=AF=4，现将△AEF沿线段EF折起到△A′EF位置，使得A′C=2