题目内容
18．用二分法研究函数f（x）=x3-2x-1的理念时，若零点所在的初始区间为（1，2），则下一个有解区间为（ ）| A． | （1，2） | B． | （1.75，2） | C． | （1.5，2） | D． | （1，1.5） |
分析 构造函数f（x）=x3-2x-1，确定f（1），f（2），f（1.5）的符号，根据零点存在定理，即可得到结论．
解答 解：设函数f（x）=x3-2x-1，
∵f（1）=-2＜0，f（2）=3＞0，f（1.5）=-$\frac{5}{8}$＜0，
∴下一个有根区间是（1.5，2），
故选：C．
点评 本题考查二分法，考查零点存在定理，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
9．已知圆M：（x-a）2+y2=4（a＞0）与圆N：x2+（y-1）2=1外切，则直线x-y-$\sqrt{2}$=0被圆M截得线段的长度为（ ）
| A． | 1 | B． | $\sqrt{3}$ | C． | 2 | D． | 2$\sqrt{3}$ |
6．下列说法正确的是（ ）
| A． | “若a＞1，则a2＞1”的否命题是“若a＞1，则a2≤1” | |
| B． | 在△ABC中，“A＞B”是“sin2A＞sin2B”必要不充分条件 | |
| C． | “若tanα$≠\sqrt{3}$，则$α≠\frac{π}{3}$”是真命题 | |
| D． | ?x0∈（-∞，0）使得3${\;}^{{x}_{0}}$＜4${\;}^{{x}_{0}}$成立 |
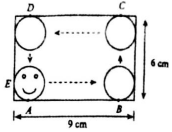有一个电动玩具，它有一个9×6的长方形（单位：cm）和一个半径为1cm的小圆盘（盘中娃娃脸），他们的连接点为A，E，打开电源，小圆盘沿着长方形内壁，从点A出发不停地滚动（无滑动），如图所示，若此时某人向该长方形盘投掷一枚飞镖，则能射中小圆盘运行区域内的概率为$\frac{40+π}{54}$．
3．要得到y=sin$\frac{x}{2}$的图象，只需将y=cos（$\frac{x}{2}$-$\frac{π}{4}$）的图象上的所有点（ ）
| A． | 向右平移$\frac{π}{2}$ | B． | 向左平移$\frac{π}{2}$ | C． | 向左平移$\frac{π}{4}$ | D． | 向右平移$\frac{π}{4}$ |