题目内容
设数列{an}是首项为1的正项数列,且(n+1)an+12-nan2+an+1an=0(n∈N*).
(1)写出数列的前五项;
(2)求数列的通项公式.
(1)写出数列的前五项;
(2)求数列的通项公式.
考点:数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件,利用递推公式,能够依次求出数列的前五项.
(2)由已知得an+1=
an=
an,由an>0,得an+1=
an,由此利用累乘法能求出数列的通项公式.
(2)由已知得an+1=
-1±
| ||
| 2(n+1) |
| -1±(2n+1) |
| 2(n+1) |
| n |
| n+1 |
解答:
解:(1)∵(n+1)an+12-nan2+an+1an=0,首项为a1=1,
∴2a22-1+a2=0,解得a2=
,或a2=-1(舍),
3a32-2×
+
a3=0,解得a3=
,或a3=-
(舍),
4a42-3×
+
a4=0,解得a4=
,或a4=-
(舍),
5a52-4×
+
a5=0,解得a5=
,或a5=-
(舍),
∴数列的前五项为1,
,
,
,
.
(2)∵(n+1)an+12-nan2+an+1an=0,首项为a1=1,
∴an+1=
an=
an,
∵an>0,∴an+1=
an,
∴an=a1×
×
×
×…×
=1×
×
×…×
=
.
故an=
.
∴2a22-1+a2=0,解得a2=
| 1 |
| 2 |
3a32-2×
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
4a42-3×
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
5a52-4×
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4 |
∴数列的前五项为1,
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
(2)∵(n+1)an+12-nan2+an+1an=0,首项为a1=1,
∴an+1=
-1±
| ||
| 2(n+1) |
| -1±(2n+1) |
| 2(n+1) |
∵an>0,∴an+1=
| n |
| n+1 |
∴an=a1×
| a2 |
| a1 |
| a3 |
| a2 |
| a4 |
| a3 |
| an |
| an-1 |
=1×
| 1 |
| 2 |
| 2 |
| 3 |
| n-1 |
| n |
| 1 |
| n |
故an=
| 1 |
| n |
点评:本题主要考查数列递推关系式的应用和累乘法.求数列通项公式的一般方法:公式法、累加法、累乘法、构造法等要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
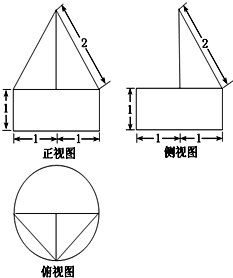
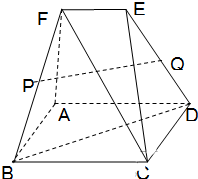 如图,多面体ABCDEF中,四边形ABCD是边长为2a的正方形,平面ADEF垂直于平面ABCD,且FA⊥AD,EF∥AD,EF=AF=a.
如图,多面体ABCDEF中,四边形ABCD是边长为2a的正方形,平面ADEF垂直于平面ABCD,且FA⊥AD,EF∥AD,EF=AF=a.