题目内容
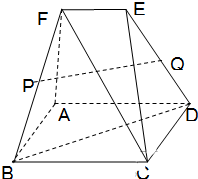 如图,多面体ABCDEF中,四边形ABCD是边长为2a的正方形,平面ADEF垂直于平面ABCD,且FA⊥AD,EF∥AD,EF=AF=a.
如图,多面体ABCDEF中,四边形ABCD是边长为2a的正方形,平面ADEF垂直于平面ABCD,且FA⊥AD,EF∥AD,EF=AF=a.(1)求证:BD⊥CF;
(2)若P、Q分别为棱BF和DE的中点,求证:PQ∥平面ABCD;
(3)求多面体ABCDEF的体积.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连结AC,由已知得BD⊥AC,FA⊥平面ABCD,BD⊥AF,由此能证明BD⊥CF.
(2)作PS⊥AB,QT⊥AD,EM⊥AD,S,T,M是垂足,由已知得四边形PSTQ是平行四边形,由此能证明PQ∥平面ABCD.
(3)多面体ABCDEF的体积V=V四棱锥P-ABCD+V三棱锥C-DEF,由此能求出结果.
(2)作PS⊥AB,QT⊥AD,EM⊥AD,S,T,M是垂足,由已知得四边形PSTQ是平行四边形,由此能证明PQ∥平面ABCD.
(3)多面体ABCDEF的体积V=V四棱锥P-ABCD+V三棱锥C-DEF,由此能求出结果.
解答:
(1)证明:连结AC,∵ABCD是正方形,∴BD⊥AC,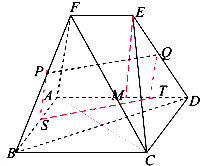
∵平面ABCD⊥平面ADEF,AF⊥AD,AD是两平面的交线,
∴FA⊥平面ABCD,而BD?平面ABCD,∴BD⊥AF,
又∵AC∩FA=A,
∴BD⊥平面AFC,而CF?平在AFC,∴BD⊥CF.
(2)证明:作PS⊥AB,QT⊥AD,EM⊥AD,S,T,M是垂足,
在△ABF中,PS:AF=BP:BF=1:2,PS=
AF,
在直角梯形中ADEF中,QT=
EM=
AF,
∴PF
QT,∴四边形PSTQ是平行四边形,∴PQ∥ST,
∴四边形PSTQ是平行四边形,∴PQ∥ST,
而ST?平面ABCD,∴PQ∥平面ABCD.
(3)解:多面体ABCDEF的体积:
V=V四棱锥P-ABCD+V三棱锥C-DEF
=
×(2a)2×a+
×
×a2×2a=
a2.

∵平面ABCD⊥平面ADEF,AF⊥AD,AD是两平面的交线,
∴FA⊥平面ABCD,而BD?平面ABCD,∴BD⊥AF,
又∵AC∩FA=A,
∴BD⊥平面AFC,而CF?平在AFC,∴BD⊥CF.
(2)证明:作PS⊥AB,QT⊥AD,EM⊥AD,S,T,M是垂足,
在△ABF中,PS:AF=BP:BF=1:2,PS=
| 1 |
| 2 |
在直角梯形中ADEF中,QT=
| 1 |
| 2 |
| 1 |
| 2 |
∴PF
| ∥ |
. |
∴四边形PSTQ是平行四边形,∴PQ∥ST,
而ST?平面ABCD,∴PQ∥平面ABCD.
(3)解:多面体ABCDEF的体积:
V=V四棱锥P-ABCD+V三棱锥C-DEF
=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 3 |
点评:本题考查异面直线垂直的证明,考查直线与平面平行的证明,考查多面体的体积的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
在长为16cm的线段AB上任取一点M,并以线段AM为一边作正方形,则此正方形的面积介于25cm2与81cm2之间的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
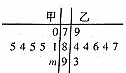 如图为甲,乙两名学生7次考试成绩的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙考试成绩的平均数分别为a和b,则一定有( )
如图为甲,乙两名学生7次考试成绩的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙考试成绩的平均数分别为a和b,则一定有( )| A、a>b |
| B、a<b |
| C、a=b |
| D、a,b的大小与m的值有关 |
在△ABC中,∠BAC=45°,AC=a,AB=
AC,E,F为边BC的三等分点,则
•
=( )
| 2 |
| AE |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|
设向量
,
,
满足
+
+
=
,且
•
=0,则|
|=3,|
|=4,则|
|=( )
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| a |
| c |
| b |
| A、5 | ||
B、
| ||
C、
| ||
| D、7 |
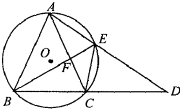 如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F.
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F.