题目内容
如图是某一个几何体的三视图，则该几何体的体积为 ．
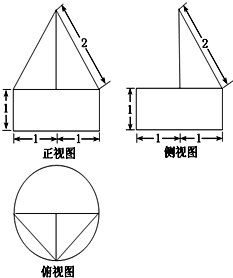
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得，该几何体是一个圆柱和棱锥的组合体，分别计算圆柱和棱锥的体积相加可得答案．
解答：
解：由已知中的三视图可得，该几何体是一个圆柱和棱锥的组合体，
圆柱的底面半径r=1，高h=1，故圆柱的体积为：π，
棱锥的底面是底边为2，高为1的三角形，高为
=
，
故棱锥的体积为：
，
故该几何体的体积为：π+
，
故答案为：π+
．
圆柱的底面半径r=1，高h=1，故圆柱的体积为：π，
棱锥的底面是底边为2，高为1的三角形，高为
| 22-12 |
| 3 |
故棱锥的体积为：
| ||
| 3 |
故该几何体的体积为：π+
| ||
| 3 |
故答案为：π+
| ||
| 3 |
点评：本题考查了由三视图求几何体的表面积和体积，根据三视图判断几何体的形状及数据所对应的几何量是解答此类问题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
记实数x1，x2，…xn中的最小数为min{x1，x2，…xn}，设函数f（x）=min{1+sinωx，1-sinωx}（ω＞0），若f（x）的最小正周期为1，则ω的值为（ ）
A、
| ||
| B、1 | ||
C、
| ||
| D、π |
在△ABC中，∠BAC=45°，AC=a，AB=
AC，E，F为边BC的三等分点，则
•
=（ ）
| 2 |
| AE |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|