题目内容
如图所示，四边形ABCD是正方形，延长CD至E，使得DE=CD．若动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，其中| AP |
| AB |
| AE |
①满足λ+μ=2的点P必为BC的中点；
②λ+μ的最小值不存在；
③满足λ+μ=1的点P有且只有一个；
④λ+μ的最大值为3．
其中正确的命题序号是：
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，取AB=1．由于
=
+
=
-
，
=λ
+μ
，可得
=(λ-μ)
+μ
=（λ-μ）（1，0）+μ（0，1）=（λ-μ，μ）．由动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，分类讨论即可得出．
| AE |
| AD |
| DE |
| AD |
| AB |
| AP |
| AB |
| AE |
| AP |
| AB |
| AD |
解答：
解：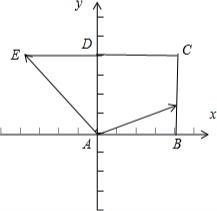
如图所示，取AB=1．
∵
=
+
=
-
，
=λ
+μ
，
∴
=(λ-μ)
+μ
=（λ-μ）（1，0）+μ（0，1）=（λ-μ，μ）．
由动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，
当P∈AB时，有0≤λ-μ≤1，μ=0，∴0≤λ≤1，0≤λ+μ≤1，
当P∈BC时，有λ-μ=1，0≤μ≤1，∴λ=μ+1，∴1≤λ≤2，
∴1≤λ+μ≤3，
当P∈CD时，有0≤λ-μ≤1，μ=1，∴μ≤λ≤μ+1，即1≤λ≤2，
∴2≤λ+μ≤3，
当P∈AD时，有λ-μ=0，0≤μ≤1，∴0≤λ≤1，∴0≤λ+μ≤2，
综上，0≤λ+μ≤3．
①取λ=μ=1满足λ+μ=2，此时
=
+
=
，因此点P不一定是BC的中点，不正确；
②当P取点A时，λ+μ取得最小值0，因此不正确；
③当点P取B或AD的中点时：满足λ+μ=1的点P不唯一，因此不正确；
④当点P取C点时，
，解得λ=2，μ=1，λ+μ取得最大值为3．
综上可知：只有④正确．
故答案为：④．
如图所示，取AB=1．∵
| AE |
| AD |
| DE |
| AD |
| AB |
| AP |
| AB |
| AE |
∴
| AP |
| AB |
| AD |
由动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，
当P∈AB时，有0≤λ-μ≤1，μ=0，∴0≤λ≤1，0≤λ+μ≤1，
当P∈BC时，有λ-μ=1，0≤μ≤1，∴λ=μ+1，∴1≤λ≤2，
∴1≤λ+μ≤3，
当P∈CD时，有0≤λ-μ≤1，μ=1，∴μ≤λ≤μ+1，即1≤λ≤2，
∴2≤λ+μ≤3，
当P∈AD时，有λ-μ=0，0≤μ≤1，∴0≤λ≤1，∴0≤λ+μ≤2，
综上，0≤λ+μ≤3．
①取λ=μ=1满足λ+μ=2，此时
| AP |
| AB |
| AE |
| AD |
②当P取点A时，λ+μ取得最小值0，因此不正确；
③当点P取B或AD的中点时：满足λ+μ=1的点P不唯一，因此不正确；
④当点P取C点时，
|
综上可知：只有④正确．
故答案为：④．
点评：本题考查了向量的坐标运算、向量的三角形法则、分类讨论的思想方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
小题狂做系列答案
相关题目
长方体ABCDA1B1C1D1的体积为V，P是DD1的中点，Q是AB上的动点，则四面体P-CDQ的体积是已知函数f（x）及其导数f′（x），若存在x0，使得f（x0）=f′（x0），则称x0是f（x）的一个“巧值点”，下列函数中，有“巧值点”的是（ ）
①f（x）=x2，
②f（x）=e-x，
③f（x）=lnx，
④f（x）=tanx，
⑤f（x）=x+
．
①f（x）=x2，
②f（x）=e-x，
③f（x）=lnx，
④f（x）=tanx，
⑤f（x）=x+
| 1 |
| x |
| A、①③⑤ | B、③④ |
| C、②③④ | D、②⑤ |
偶函数y=f（x）在区间[0，4]上单调递减，则有（ ）
| A、f（-1）＞f（2）＞f（-π） |
| B、f（-π）＞f（2）＞f（-1） |
| C、f（-1）＞f（-π）＞f（2） |
| D、f（2）＞f（-1）＞f（-π） |