题目内容
定义:若函数f(x)对于其定义域内的某一数x0,有f(x0)=x0,则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=2,b=7时,求函数f(x)的不动点;
(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上两个点A、B的横坐标是函数f(x)的不动点,且A、B的中点C在函数g(x)=-x+
的图象上,求b的最小值.
(1)当a=2,b=7时,求函数f(x)的不动点;
(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上两个点A、B的横坐标是函数f(x)的不动点,且A、B的中点C在函数g(x)=-x+
| a |
| 5a2-4a+1 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)将a=2,b=7代入f(x)=ax2+(b+1)x+b-1 (a≠0),求出f(x),令f(x)=x,解方程求不动点即可;
(2)令ax2+(b+1)x+b-1=x,即方程ax2+bx+b-1=0恒有两个不等实根,所以△=b2-4a(b-1)>0即b2-4ab+4a>0对任意的b∈R恒成立,
故△'=16a2-16a<0,故0<a<1;
(3)先设出两点的坐标分别为A(x1,x1),B(x2,x2)(x1≠x2),又AB的中点C在函数在函数g(x)=-x+
的图象上,
所以
=-
+
,即x1+x2=
,而x1,x2是方程ax2+bx+b-1=0的两个根,所以x1+x2=-
至此题设中的条件转化为-
=
,观察发现参数b可以表示成参数a的函数,至此,求参数b的问题转化为求b关于a的函数最小值的问题.
(2)令ax2+(b+1)x+b-1=x,即方程ax2+bx+b-1=0恒有两个不等实根,所以△=b2-4a(b-1)>0即b2-4ab+4a>0对任意的b∈R恒成立,
故△'=16a2-16a<0,故0<a<1;
(3)先设出两点的坐标分别为A(x1,x1),B(x2,x2)(x1≠x2),又AB的中点C在函数在函数g(x)=-x+
| a |
| 5a2-4a+1 |
所以
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| a |
| 5a2-4a+1 |
| a |
| 5a2-4a+1 |
| b |
| a |
至此题设中的条件转化为-
| b |
| a |
| a |
| 5a2-4a+1 |
解答:
解:(1)f(x)=2x2+8x+6=x,解得x=-2或x=-
.所以所求的不动点为-2或-
.
(2)令ax2+(b+1)x+b-1=x,即方程ax2+bx+b-1=0恒有两个不等实根,
所以△=b2-4a(b-1)>0即b2-4ab+4a>0对任意的b∈R恒成立,
故△'=16a2-16a<0,故0<a<1
(3)设A(x1,x1),B(x2,x2)x1≠x2,
又AB的中点C在函数在函数g(x)=-x+
的图象上,
所以
=-
+
,即x1+x2=
而x1,x2是方程ax2+bx+b-1=0的两个根,所以x1+x2=-
即-
=
所以b=-
=-
=-
由(2)知:0<a<1
则当
=2,即a=
时bmin=-1
| 3 |
| 2 |
| 3 |
| 2 |
(2)令ax2+(b+1)x+b-1=x,即方程ax2+bx+b-1=0恒有两个不等实根,
所以△=b2-4a(b-1)>0即b2-4ab+4a>0对任意的b∈R恒成立,
故△'=16a2-16a<0,故0<a<1
(3)设A(x1,x1),B(x2,x2)x1≠x2,
又AB的中点C在函数在函数g(x)=-x+
| a |
| 5a2-4a+1 |
所以
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| a |
| 5a2-4a+1 |
| a |
| 5a2-4a+1 |
而x1,x2是方程ax2+bx+b-1=0的两个根,所以x1+x2=-
| b |
| a |
即-
| b |
| a |
| a |
| 5a2-4a+1 |
所以b=-
| a2 |
| 5a2-4a+1 |
| 1 | ||||
(
|
| 1 | ||
(
|
由(2)知:0<a<1
则当
| 1 |
| a |
| 1 |
| 2 |
点评:本题考点是二次函数的性质,主要考查二次函数、方程的基本性质、不等式的有关知识,同时考查函数思想、数形结合思想、逻辑推理能力和创新意识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知点O在△ABC内,且2
+3
+6
=
,那么△OBC、△OCA、△OAB的面积之比为( )
| OA |
| OB |
| OC |
| 0 |
| A、1:2:3 |
| B、2:3:6 |
| C、3:2:1 |
| D、6:3:2 |
已知向量
=(x1,y1),
=(x2,y2),若|
|=2,|
|=3,
•
=-6,并且x2+y2≠0,则
的值是( )
| a |
| b |
| a |
| b |
| a |
| b |
| x1+y1 |
| x2+y2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
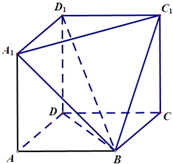 如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.
如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.