题目内容
已知点O在△ABC内,且2
+3
+6
=
,那么△OBC、△OCA、△OAB的面积之比为( )
| OA |
| OB |
| OC |
| 0 |
| A、1:2:3 |
| B、2:3:6 |
| C、3:2:1 |
| D、6:3:2 |
考点:三角形的面积公式
专题:平面向量及应用
分析:如图所示,分别延长OA,OB,OC至A′,B′,C′点,使得
=2
,
=3
,
=6
,由于2
+3
+6
=
,可得
+
+
=
,延长点O是△A′B′C′的重心.可得△OB′C′、△OC′A′、△OA′B′的面积相等.于是
=
=
,S△OAB=
S△A′B′C′,同理可得S△OAC=
S△A′B′C′,S△OBC=
S△A′B′C′.即可得出.
| OA′ |
| OA |
| OB′ |
| OB |
| OC′ |
| OC |
| OA |
| OB |
| OC |
| 0 |
| OA′ |
| OB′ |
| OC′ |
| 0 |
| S△OAB |
| S△OA′B′ |
| ||
|
| 1 |
| 6 |
| 1 |
| 18 |
| 1 |
| 36 |
| 1 |
| 54 |
解答:
解:如图所示,分别延长OA,OB,OC至A′,B′,C′点,使得
=2
,
=3
,
=6
,
∵2
+3
+6
=
,∴
+
+
=
,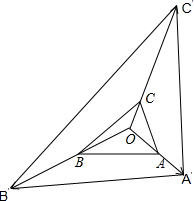
∴点O是△A′B′C′的重心.
∴△OB′C′、△OC′A′、△OA′B′的面积相等.
∵
=
=
×
=
,
∴S△OAB=
S△A′B′C′,
同理可得S△OAC=
S△A′B′C′,
S△OBC=
S△A′B′C′.
∴△OBC、△OCA、△OAB的面积之比为2:3:6.
故选:B.
| OA′ |
| OA |
| OB′ |
| OB |
| OC′ |
| OC |
∵2
| OA |
| OB |
| OC |
| 0 |
| OA′ |
| OB′ |
| OC′ |
| 0 |

∴点O是△A′B′C′的重心.
∴△OB′C′、△OC′A′、△OA′B′的面积相等.
∵
| S△OAB |
| S△OA′B′ |
| ||
|
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
∴S△OAB=
| 1 |
| 18 |
同理可得S△OAC=
| 1 |
| 36 |
S△OBC=
| 1 |
| 54 |
∴△OBC、△OCA、△OAB的面积之比为2:3:6.
故选:B.
点评:本题考查了三角形重心的性质定理、三角形面积计算公式、向量的共线定理,考查了推理能力与计算能力,考查了数形结合的能力,属于难题.

练习册系列答案
相关题目
在各项均为正数的等比数列{an}中,
≤2,则下列结论中正确的是( )
| a3+a11 |
| a7 |
| A、数列{an}是常数列 |
| B、数列{an}是递增数列 |
| C、数列{an}是递减数列 |
| D、数列{an}有可能是递增数列也有可能是递减数列 |