题目内容
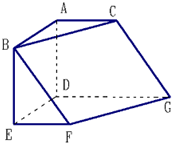 在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形ABED是矩形,四边形ADGC是直角梯形,∠ADG=90°,四边形DEFG是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.
在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形ABED是矩形,四边形ADGC是直角梯形,∠ADG=90°,四边形DEFG是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.(1)求证:FG⊥面ADF;
(2)求四面体CDFG的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)首先,作DG的中点为H,证明四边形DEFH为平行四边形,然后,得到AD⊥平面EDGF,从而得证;
(2)先证明CO⊥平面EDGF,(取DG的中点为O),得到△DEF正三角形,然后,结合四面体CDFG的体积V=
S△DFG•CO进行求解.
(2)先证明CO⊥平面EDGF,(取DG的中点为O),得到△DEF正三角形,然后,结合四面体CDFG的体积V=
| 1 |
| 3 |
解答:
解:(1)连接DF,AF,作DG的中点为H,连接EH,
∵EF∥DK,EF=DH=ED=1,
∴四边形DEFH为菱形,
∴EF∥HG,EF=HG,
∴四边形DEFH为平行四边形,
∴FG∥EH,
∴FG⊥DF,
∵∠ADG=90°,AD⊥DG,AD⊥ED,
∴AD⊥平面EDGF,
∴AD⊥FG,
∵FG⊥DF,AD∩DF=D,
∴FG⊥面ADF;
(2)取DG的中点为O,连接FO,CO,FD,
∵DO∥AC,DO=AC,
∴ADOC平行四边形,
∴CO∥AD,CO=AD=1,
根据(1)知,AD⊥平面EDGF,
∴CO⊥平面EDGF,
∴ED=EF=1,∠DEF=60°,
∴△DEF正三角形,
∴DF=1,∠FDG=60°,
∴S△DFG=
•DF•DG•sin∠FDG=
,
∴四面体CDFG的体积V=
S△DFG•CO=
×
×1=
.
∵EF∥DK,EF=DH=ED=1,
∴四边形DEFH为菱形,
∴EF∥HG,EF=HG,
∴四边形DEFH为平行四边形,
∴FG∥EH,
∴FG⊥DF,
∵∠ADG=90°,AD⊥DG,AD⊥ED,
∴AD⊥平面EDGF,
∴AD⊥FG,
∵FG⊥DF,AD∩DF=D,
∴FG⊥面ADF;
(2)取DG的中点为O,连接FO,CO,FD,
∵DO∥AC,DO=AC,
∴ADOC平行四边形,
∴CO∥AD,CO=AD=1,
根据(1)知,AD⊥平面EDGF,
∴CO⊥平面EDGF,
∴ED=EF=1,∠DEF=60°,
∴△DEF正三角形,
∴DF=1,∠FDG=60°,
∴S△DFG=
| 1 |
| 2 |
| ||
| 2 |
∴四面体CDFG的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
点评:本题重点考查了空间中平行关系和垂直关系的判断方法、空间几何体的体积求解等知识,属于中档题.

练习册系列答案
相关题目
 如图所示的电路图,设命题p:开关K闭合,命题q:开关K1闭合,命题s:开关K2闭合,命题t:开关K3闭合.
如图所示的电路图,设命题p:开关K闭合,命题q:开关K1闭合,命题s:开关K2闭合,命题t:开关K3闭合.