题目内容
求下列函数最值及相应的x值:
(1)y=x+
(x>1)的最小值及相应的x值.
(2)y=2x•(1-x)(0<x<1)的最大值及相应的x值.
(1)y=x+
| 1 |
| x-1 |
(2)y=2x•(1-x)(0<x<1)的最大值及相应的x值.
考点:基本不等式
专题:不等式的解法及应用
分析:(1)(2)变形利用基本不等式的性质即可得出.
解答:
解:(1)∵x>1,∴y=x+
=x-1+
+1≥2
-1=1,当且仅当x=2时取等号,∴y=x+
(x>1)的最小值为1.
(2)∵0<x<1,∴y=2x(1-x)≤2(
)2=
,当且仅当x=
时取等号,∴y=2x•(1-x)(0<x<1)的最大值为
.
| 1 |
| x-1 |
| 1 |
| x-1 |
(x-1)•
|
| 1 |
| x-1 |
(2)∵0<x<1,∴y=2x(1-x)≤2(
| x+1-x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
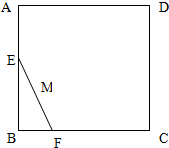 如图,线段EF的长度为1,端点E、F在边长不小于1的正方形ABCD的四边上滑动,当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为L,其围成的面积为S,则L-S的最大值为( )
如图,线段EF的长度为1,端点E、F在边长不小于1的正方形ABCD的四边上滑动,当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为L,其围成的面积为S,则L-S的最大值为( )| A、4-π | ||
B、2+
| ||
C、
| ||
| D、2π-2 |
已知某几何体的三视图如上图所示(单位:cm),则该几何体的表面积是( )
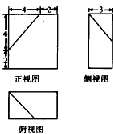

A、(124+2
| ||
| B、92cm2 | ||
| C、124cm2 | ||
| D、84cm2 |
在△ABC中,角A,B,C所对的边分别为a,b,c,S表示△ABC的面积,若acosB+bcosA=csinC,S=
(b2+c2-a2),则∠B=( )
| 1 |
| 4 |
| A、90° | B、60° |
| C、45° | D、30° |
已知等差数列{an}的前n项和为Sn,若S3=9,S5=25,则S8=( )
| A、60 | B、62 | C、64 | D、66 |
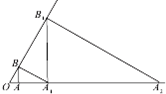 如图,在△OAB中,OA⊥AB,OB=1,OA=
如图,在△OAB中,OA⊥AB,OB=1,OA=