题目内容
已知sin(
+θ)=
,θ为锐角,则sinθ= .
| π |
| 4 |
| 4 |
| 5 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:由同角三角函数的基本关系易得cos(
+θ)的值,代入sinθ=sin[(
+θ)-
]=
sin(
+θ)-
cos(
+θ),计算可得.
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
解答:
解:∵θ为锐角,∴
<
+θ<
,
又∵sin(
+θ)=
,
∴cos(
+θ)=
,或cos(
+θ)=-
,
∴sinθ=sin[(
+θ)-
]
=
sin(
+θ)-
cos(
+θ)
当cos(
+θ)=
时,上式=
×
-
×
=
,
当cos(
+θ)=-
时,上式=
×
+
×
=
,
故答案为:
或
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
又∵sin(
| π |
| 4 |
| 4 |
| 5 |
∴cos(
| π |
| 4 |
| 3 |
| 5 |
| π |
| 4 |
| 3 |
| 5 |
∴sinθ=sin[(
| π |
| 4 |
| π |
| 4 |
=
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
当cos(
| π |
| 4 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| ||
| 10 |
当cos(
| π |
| 4 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
7
| ||
| 10 |
故答案为:
| ||
| 10 |
7
| ||
| 10 |
点评:本题考查两角和与差的三角函数公式,涉及同角三角函数的基本关系,属基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
设x,y满足约束条件
且z=x+ay的最小值为7,则a=( )
|
| A、-5 | B、3 |
| C、-5或3 | D、5或-3 |
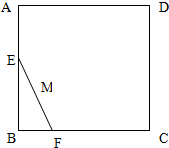 如图,线段EF的长度为1,端点E、F在边长不小于1的正方形ABCD的四边上滑动,当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为L,其围成的面积为S,则L-S的最大值为( )
如图,线段EF的长度为1,端点E、F在边长不小于1的正方形ABCD的四边上滑动,当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为L,其围成的面积为S,则L-S的最大值为( )| A、4-π | ||
B、2+
| ||
C、
| ||
| D、2π-2 |
下列各式错误的是( )
| A、tan138°<tan143° | ||||
B、sin(-
| ||||
| C、lg1.6>lg1.4 | ||||
| D、0.75-0.1<0.750.1 |
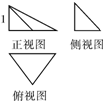 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积是( )| A、36π | ||
| B、9π | ||
C、
| ||
D、
|
在△ABC中,角A,B,C所对的边分别为a,b,c,S表示△ABC的面积,若acosB+bcosA=csinC,S=
(b2+c2-a2),则∠B=( )
| 1 |
| 4 |
| A、90° | B、60° |
| C、45° | D、30° |