题目内容
已知P、M、N是单位圆上互不相同的三个点,且满足|
|=|
|,则
•
的最小值是 ( )
| PM |
| PN |
| PM |
| PN |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-1 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由题意可得,点P在MN的垂直平分线上,不妨设单位圆的圆心为O(0,0),点P(0,1),点M(x1,y1),则点N(-x1,y1),由x12+y12=1得
•
=2y12-2y1,求出最小值.
| PM |
| PN |
解答:
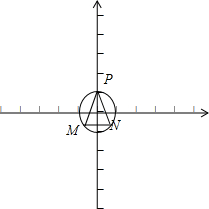 解:由题意可得,点P在MN的垂直平分线上,不妨设单位圆
解:由题意可得,点P在MN的垂直平分线上,不妨设单位圆
的圆心为O(0,0),
点P(0,1),点M(x1,y1),则点N(-x1,y1),
-1≤y1<1
∴
=(x1,y1-1),
=(-x1,y1-1),
x12+y12=1.
∴
•
=-x12+y12-2y1+1
=2y12-2y1=2(y1-
)2-
,
∴当y1=
时
•
的最小值是-
故选:B.
 解:由题意可得,点P在MN的垂直平分线上,不妨设单位圆
解:由题意可得,点P在MN的垂直平分线上,不妨设单位圆的圆心为O(0,0),
点P(0,1),点M(x1,y1),则点N(-x1,y1),
-1≤y1<1
∴
| PM |
| PN |
x12+y12=1.
∴
| PM |
| PN |
=2y12-2y1=2(y1-
| 1 |
| 2 |
| 1 |
| 2 |
∴当y1=
| 1 |
| 2 |
| PM |
| PN |
| 1 |
| 2 |
故选:B.
点评:本题主要考查两个向量的数量积公式,二次函数的性质,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
定义a⊕b=
,设函数f(x)=lnx⊕x,则f(2)+f(
)=( )
|
| 1 |
| 2 |
| A、4ln2 | B、-4ln2 |
| C、2 | D、0 |
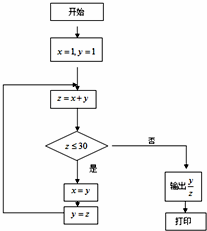
如图所示计算机程序的打印结果为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
过点A(2,b)和点B(3,-2)的直线的倾斜角为
,则b的值是( )
| 3π |
| 4 |
| A、-1 | B、1 | C、-5 | D、5 |
在平面直角坐标系xOy中,已知平面向量
=(a,0),
=(0,b),其中a,b为[-2,2]上的两个随机实数,定义平面上的点集Ω,Ω1,Φ分别为Ω={P|
=
+
},Ω1={Q|
|=|
|=
且|QP|<1,P∈Ω},Φ:Ω1∪{R|
<|
|<2}.若在Ω对应的平面区域内随机取一个点W,则点W落在Φ对应的平面区域内的概率为( )
| ON1 |
| ON2 |
| OP |
| ON1 |
| ON2 |
| QN1 |
| QN2 |
| 2 |
| 3 |
| OR |
A、
| ||
B、1-
| ||
C、
| ||
D、
|
关于x的不等式ax2+2ax-4<0对一切x∈R恒成立,则a的取值范围是( )
| A、(-4,0) |
| B、(-4,0] |
| C、[-4,0) |
| D、[-4,0] |
若x=
,则sin4x-cos4x的值为( )
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
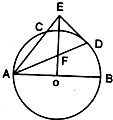 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.求证:ED是⊙O的切线.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.求证:ED是⊙O的切线.