题目内容
关于x的不等式ax2+2ax-4＜0对一切x∈R恒成立，则a的取值范围是（ ）
| A、（-4，0） |
| B、（-4，0] |
| C、[-4，0） |
| D、[-4，0] |
考点：函数恒成立问题
专题：综合题,不等式的解法及应用
分析：当a=0时，不等式对一切x∈R恒成立，当aa≠0时，由二次项系数小于0且对应的判别式小于0联立不等式组求解a的范围，最后把a取并集得答案．
解答：
解：当a=0时，不等式化为-4＜0，满足题意；
当a≠0时，则：
，解得：-4＜a＜0．
综上，满足ax2+2ax-4＜0对一切x∈R恒成立的实数a的取值范围是（-4，0]．
故选：B．
当a≠0时，则：
|
综上，满足ax2+2ax-4＜0对一切x∈R恒成立的实数a的取值范围是（-4，0]．
故选：B．
点评：本题考查了函数恒成立问题，考查了二次不等式的解法，训练了“三个二次”在解题中的应用，是中档题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
函数f（x）=4sin（4x-
）是（ ）
| 5π |
| 2 |
| A、周期为π的奇函数 | ||
| B、周期为π的偶函数 | ||
C、周期为
| ||
D、周期为
|
△ABC中，A＞B是sinB＜sinA成立的（ ）条件．
| A、必要不充分 | B、充分不必要 |
| C、充要 | D、不充分不必要 |
已知f（x），g（x）都是定义在R上的函数，g（x）≠0，f′（x）g（x）＜f（x）g′（x），f（x）=axg（x），
+
=
，则
=（ ）
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 10 |
| 3 |
| f(2) |
| g(2) |
| A、a2 | ||
B、
| ||
| C、9 | ||
D、
|
已知P、M、N是单位圆上互不相同的三个点，且满足|
|=|
|，则
•
的最小值是 （ ）
| PM |
| PN |
| PM |
| PN |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-1 |
设函数f（x）是R上以4为周期的可导偶函数，则曲线y=f（x）在x=4处的切线的斜率为（ ）
A、-
| ||
| B、0 | ||
C、
| ||
| D、4 |
函数y=
sin（2x-
）的图象可以看作是把函数y=
sin2x的图象（ ）
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
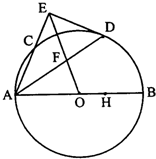如图，AB是⊙O的直径，AC是弦，∠BAC的平分线交⊙O于D，DE⊥AC，交AC的延长线于E，OE交AD于F．