题目内容
甲、乙、丙三人参加一项技能测试,已知甲通过测试的概率为
,乙通过测试的概率为
,乙、丙两人同时通过测试的概率为
,且三人能否通过测试相互独立.
(1)求三人中至少一人通过测试的概率;
(2)设X为甲、乙、丙三人中通过测试的人数,求X的分布列和数学期望.
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
(1)求三人中至少一人通过测试的概率;
(2)设X为甲、乙、丙三人中通过测试的人数,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)由已知条件求出丙通过的概率,由此利用对立事件的概率能求出三人中至少一人通过测试的概率.
(2)由题意知X=0,1,2,3,分别求出相对应的概率,由此能求出X的分布列和EX.
(2)由题意知X=0,1,2,3,分别求出相对应的概率,由此能求出X的分布列和EX.
解答:
解:(1)设丙通过的概率为x,
∵乙通过测试的概率为
,乙、丙两人同时通过测试的概率为
,且三人能否通过测试相互独立.
∴
x=
,∴x=
,
∵甲通过测试的概率为
,∴三人中至少一人通过测试的概率:
p=1-(1-
)(1-
)(1-
)=
.
(2)由题意知X=0,1,2,3,
P(X=0)=(1-
)(1-
)(1-
)=
,
P(X=1)=
(1-
)(1-
)+(1-
)•
•(1-
)+(1-
)(1-
)•
=
,
P(X=2)=
•
•(1-
)+
•(1-
)•
+(1-
)•
•
=
,
P(X=3)=
×
×
=
,
∴X的分布列为:
EX=0×
+1×
+2×
+3×
=
.
∵乙通过测试的概率为
| 1 |
| 2 |
| 1 |
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
∵甲通过测试的概率为
| 3 |
| 5 |
p=1-(1-
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 14 |
| 15 |
(2)由题意知X=0,1,2,3,
P(X=0)=(1-
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 15 |
P(X=1)=
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 10 |
P(X=2)=
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 13 |
| 30 |
P(X=3)=
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 5 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 15 |
| 3 |
| 10 |
| 13 |
| 30 |
| 1 |
| 5 |
| 53 |
| 30 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
 已知正四面体的俯视图如图所示,其中ABCD是边长为2的正方形,则这个正四面体的体积为( )
已知正四面体的俯视图如图所示,其中ABCD是边长为2的正方形,则这个正四面体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知P、M、N是单位圆上互不相同的三个点,且满足|
|=|
|,则
•
的最小值是 ( )
| PM |
| PN |
| PM |
| PN |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-1 |
函数y=
sin(2x-
)的图象可以看作是把函数y=
sin2x的图象( )
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
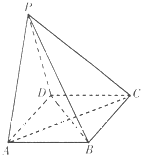 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=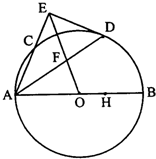 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F.
