题目内容
某校进入高中数学竞赛复赛的学生中,高一年级有6人,高二年级有12人,高三年级有24人,现采用分层抽样的方法从这些学生中抽取7人进行采访
(Ⅰ)求应从各年级分别抽取的人数:
(Ⅱ)若从抽取的7人中再随机抽取2人做进一步了解
(i)列出所有可能的抽取结果;
(ii)求抽取的2人均为高三年级学生的概率.
(Ⅰ)求应从各年级分别抽取的人数:
(Ⅱ)若从抽取的7人中再随机抽取2人做进一步了解
(i)列出所有可能的抽取结果;
(ii)求抽取的2人均为高三年级学生的概率.
考点:分层抽样方法
专题:概率与统计
分析:(Ⅰ)根据方差抽样的定义即可求应从各年级分别抽取的人数:
(Ⅱ)根据古典概型的概率公式即可求出对应的概率.
(Ⅱ)根据古典概型的概率公式即可求出对应的概率.
解答:
解:(Ⅰ)∵高一,高二,高三的人数比为6:12:24=1:2:4,
则用分层抽样的方法从这些学生中抽取7人,则高一,高二,高三的人数分别为1,2,4.
(Ⅱ)若从抽取的7人中高一学生记为a,高二的两个学生记为b,c,高三的两个学生记为A,B,C,D,
则抽取2人的结果是(a,b),(a,c),(a,A),(a,B),(a,C),(a,D),
(b,c),(b,A),(b,B),(b,C),(b,D),
(c,A),(c,B),(c,C),(c,D),
(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),共21种结果.
抽取的2人均为高三年级学生(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),共6种结果.
则抽取的2人均为高三年级学生的概率P=
=
.
则用分层抽样的方法从这些学生中抽取7人,则高一,高二,高三的人数分别为1,2,4.
(Ⅱ)若从抽取的7人中高一学生记为a,高二的两个学生记为b,c,高三的两个学生记为A,B,C,D,
则抽取2人的结果是(a,b),(a,c),(a,A),(a,B),(a,C),(a,D),
(b,c),(b,A),(b,B),(b,C),(b,D),
(c,A),(c,B),(c,C),(c,D),
(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),共21种结果.
抽取的2人均为高三年级学生(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),共6种结果.
则抽取的2人均为高三年级学生的概率P=
| 6 |
| 21 |
| 2 |
| 7 |
点评:本题主要考查分层抽样的应用以及古典概率的计算,利用列举法是解决本题概型的基本方法.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设f(x)=ax2+bx+c(a,b,c∈R),e为自然对数的底数.若f′(x)lnx>
.则( )
| f(x) |
| x |
| A、f(2)<f(e)ln2,2f(e)>f(e2) |
| B、f(2)<f(e)ln2,2f(e)<f(e2) |
| C、f(2)>f(e)ln2,2f(e)<f(e2) |
| D、f(2)>f(e)ln2,2f(e)>f(e2) |
圆C:(x+1)2+(y-3)2=9上有两点P,Q关于直线x+my+4=0对称,则m等于( )
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
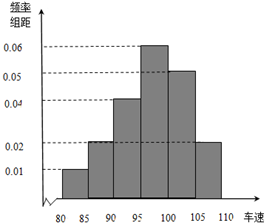 2013年国庆期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.
2013年国庆期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.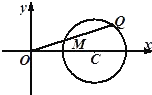 (理科)如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点.
(理科)如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点.