题目内容
 如图,f(x)=Asin(2ωx+φ)(ω>0,A>0,-π<φ<0).
如图,f(x)=Asin(2ωx+φ)(ω>0,A>0,-π<φ<0).(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)在[-π,-
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)通过函数的图象得到A,T,求出ω,利用函数图象经过(0,-1)结合-π<φ<0求出φ,得到函数的解析式.
(Ⅱ)通过x∈[-π,-
],求出相位的范围,利用正弦函数的值域求出函数的值域.
(Ⅱ)通过x∈[-π,-
| π |
| 2 |
解答:
解:(Ⅰ)如图:A=2,T=
(
+
)=π,∴T=π.
由周期公式得2ω=
=2
∴f(x)=2sin(2x+φ)
又∵f(x)的图象过( 0,-1)
∴2sinφ=-1
又∵-π<φ<0
∴φ=-
∴f(x)=2sin(2x-
).
(Ⅱ)∵
x∈[-π,-
],∴2x-
∈[-
,-
],
∴2sin(2x-
)∈[-2,1].
∴函数f(x)在[-π,-
]上的值域为:[-2,1].
| 4 |
| 3 |
| 2π |
| 3 |
| π |
| 12 |
由周期公式得2ω=
| 2π |
| T |
∴f(x)=2sin(2x+φ)
又∵f(x)的图象过( 0,-1)
∴2sinφ=-1
又∵-π<φ<0
∴φ=-
| 5π |
| 6 |
∴f(x)=2sin(2x-
| 5π |
| 6 |
(Ⅱ)∵
x∈[-π,-
| π |
| 2 |
| 5π |
| 6 |
| 17π |
| 6 |
| 11π |
| 6 |
∴2sin(2x-
| 5π |
| 6 |
∴函数f(x)在[-π,-
| π |
| 2 |
点评:本题主要考查三角函数图象与解析式中各参数的内在联系,培养学生知图求式,以式知图的能力,计算能力.

练习册系列答案
相关题目
设|
|=2,|
|=3,∠BAC=60°,
=2
,
=x
+(1+x)
,x∈[0,1],则
在
上的投影的取值范围是( )
| AB |
| AC |
| CD |
| BC |
| AE |
| AD |
| AB |
| AE |
| AC |
| A、[0,1] |
| B、[0,7] |
| C、[1,9] |
| D、[9,21] |
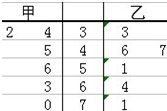 近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.其形成与PM2.5有关.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部于2012年2月29日,发布了《环境空气质量标准》见表:
近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.其形成与PM2.5有关.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部于2012年2月29日,发布了《环境空气质量标准》见表: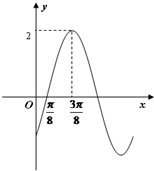 函数f(x)=Msin(ωx-
函数f(x)=Msin(ωx-