题目内容
9. 如图,在三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,在三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.(Ⅰ)如果CD=$\sqrt{2}$,求证:平面BCE⊥平面ABD;
(Ⅱ)如果∠CBD=$\frac{2π}{3}$,求直线CE和平面BCD所成的角的余弦值.
分析 (Ⅰ)推导出BC⊥BD,AB⊥BC.由此能证明平面BCE⊥平面ABD.
(Ⅱ) 取线段BD的中点G,连接EG,CG,推导出EG⊥平面BCD,∠ECG为直线CE和平面BCD所成的角,由此能求出直线CE和平面BCD所成的角的余弦值.
解答 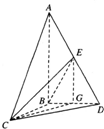 证明:(Ⅰ)∵$BC=BD=1,CD=\sqrt{2}$,
证明:(Ⅰ)∵$BC=BD=1,CD=\sqrt{2}$,
∴BC2+BD2=CD2,∴BC⊥BD.…(2分)
∵AB⊥平面BCD,BC?平面BCD,∴AB⊥BC.
又∵AB∩BD=B,∴BC⊥平面ABD.…(4分)
又BC?平面BCE,
∴平面BCE⊥平面ABD…(6分)
解:(Ⅱ) 取线段BD的中点G,连接EG,CG.
在△ABD中,∵AE=ED,BG=GD,
∴EG∥AB.∵AB⊥平面BCD,∴EG⊥平面BCD…(8分)
∴直线EC在平面BCD内的射影为CG,
∠ECG为直线CE和平面BCD所成的角…(9分)
在△ABD中,$EG=\frac{1}{2}AB=\frac{{\sqrt{3}}}{2}$.
在△BCD中,$C{G^2}=B{C^2}+B{G^2}-2BC•BG•cos\frac{2π}{3}=\frac{7}{4}$,CG=$\frac{{\sqrt{7}}}{2}$.
在△ECG中,$E{C^2}=E{G^2}+C{G^2}=\frac{5}{2}$,∴$EC=\frac{{\sqrt{10}}}{2}$.
在Rt△ECG中,$cos∠ECG=\frac{CG}{CE}=\frac{{\sqrt{70}}}{10}$,
∴直线CE和平面BCD所成的角的余弦值为$\frac{\sqrt{70}}{10}$.…(12分)
点评 本题考查面面垂直的证明,考查线面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下:
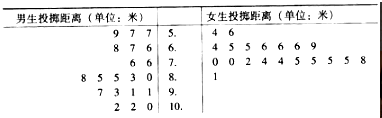
已知该项目评分标准为:
注:满分10分,且得9分以上(含9分)定为“优秀”.
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)

已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)
4.已知某正方体的外接球的表面积是16π,则这个正方体的棱长是( )
| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
14.某工厂加工某种零件的三道供需流程图如图所示,则该种零件可导致废品的环节有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.给出如图所示的一组等式,则观察图中所展示的规律,可推出S20的值为( )

| A. | 4410 | B. | 4010 | C. | 4020 | D. | 4400 |