题目内容
13.已知f(x)是定义在R上的奇函数,当x≤0时,f(x)=(x+2)e-x-2(其中e是自然对数的底数,e=2.71828…).(Ⅰ) 当x>0时,求f(x)的解析式;
(Ⅱ) 若x∈[0,2]时,方程f(x)=m有实数根,求实数m的取值范围.
分析 (Ⅰ) 利用函数的奇偶性转化求解函数的解析式即可.
(Ⅱ) 通过当x=0时,当0<x≤2时,当0<x<1时,求出函数的零点,极值,然后求解实数m的取值范围.
解答 解:(Ⅰ) 当x≤0时,f(x)=(x+2)e-x-2,
当x>0时,则-x<0时,f(-x)=(-x+2)ex-2,
由于f(x)奇函数,则f(x)=-f(-x)=-[(-x+2)ex-2],
故当x>0时,f(x)=(x-2)ex+2.(6分)
(Ⅱ) 当x=0时,f(0)=0.
当0<x≤2时,f(x)=(x-2)ex+2,f'(x)=(x-1)ex,由f'(x)=0,得x=1,
当0<x<1时,f'(x)<0,当1<x<2时,f'(x)>0,则f(x)在(0,1)上单调递减;
在(1,2)上单调递增.则f(x)在x=1处取得极小值f(1)=2-e,(10分)
又f(0)=0,f(2)=2,故当0<x≤2时,f(x)∈[2-e,2].
综上,当x∈[0,2]时,f(x)∈[2-e,2],
所以实数m的取值范围是[2-e,2].(12分)
点评 本题考查函数的导数的应用,函数的单调性以及函数的极值,考查分类讨论思想的应用,是中档题.

练习册系列答案
相关题目
3.设$f(x)=sin(x+\frac{π}{3});a=f(\frac{π}{12}),b=f(\frac{π}{6}),c=f(\frac{π}{3})$,则( )
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | b>a>c |
4.若不等式x2-2ax+a>0,对x∈R恒成立,则实数a取值范围为( )
| A. | {a|1<a<2} | B. | {a|-2<a<1} | C. | {a|0<a<2} | D. | {a|0<a<1} |
1.已知a=x2+x+$\sqrt{2}$,b=lg3,$c={e^{-\frac{1}{2}}}$,则a,b,c的大小关系为( )
| A. | a<b<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
8.已知函数f(x)=$\left\{\begin{array}{l}{(1-x)^{3},x<1}\\{(x-1)^{3},x≥1}\end{array}\right.$,若关于x的不等式f(x2-2x+2)<f(1-a2x2)的解集中有且仅有三个整数,则实数a的取值范围是( )
| A. | [-$\frac{3}{4}$,-$\frac{2}{3}$)∪($\frac{2}{3}$,$\frac{3}{4}$] | B. | ($\frac{2}{3}$,$\frac{3}{4}$] | C. | [-$\frac{3}{4}$,-$\frac{1}{2}$)∪($\frac{1}{2}$,$\frac{3}{4}$] | D. | [-$\frac{4}{5}$,-$\frac{3}{4}$)∪($\frac{3}{4}$,$\frac{4}{5}$] |
2.下列说法的正确的是( )
| A. | 经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示 | |
| B. | 经过定点A(0,b)的直线都可以用方程y=kx+b表示 | |
| C. | 不经过原点的直线都可以用方程$\frac{x}{a}$+$\frac{y}{b}$=1表示P1(x1,y1)、P2(x2,y2) | |
| D. | 经过任意两个不同的点的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)来表示 |
19.某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下:
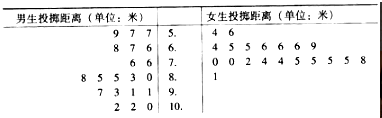
已知该项目评分标准为:
注:满分10分,且得9分以上(含9分)定为“优秀”.
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)

已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)