题目内容
14．抛物线C：y2=16x，C与直线l：y=x-4交于A，B两点，则AB中点到y轴距离为12．分析 把直线与抛物线的方程联立，消去y得到一个关于x的一元二次方程，利用根与系数的关系求出两根之和x1+x2，即可求出AB中点到y轴距离．
解答 解：把直线方程与抛物线方程联立得$\left\{\begin{array}{l}{{y}^{2}=16x}\\{y=x-4}\end{array}\right.$，
消去y得到x2-24x+16=0，利用根与系数的关系得到x1+x2=24，
∴AB中点到y轴距离为12，
故答案为：12．
点评 考查学生会求直线与抛物线的交点坐标，灵活运用根与系数的关系及中点坐标公式化简求值．
练习册系列答案
相关题目
4．若不等式x2-2ax+a＞0，对x∈R恒成立，则实数a取值范围为（ ）
| A． | {a|1＜a＜2} | B． | {a|-2＜a＜1} | C． | {a|0＜a＜2} | D． | {a|0＜a＜1} |
2．下列说法的正确的是（ ）
| A． | 经过定点P0（x0，y0）的直线都可以用方程y-y0=k（x-x0）表示 | |
| B． | 经过定点A（0，b）的直线都可以用方程y=kx+b表示 | |
| C． | 不经过原点的直线都可以用方程$\frac{x}{a}$+$\frac{y}{b}$=1表示P1（x1，y1）、P2（x2，y2） | |
| D． | 经过任意两个不同的点的直线都可以用方程（y-y1）（x2-x1）=（x-x1）（y2-y1）来表示 |
定义：f1（x）=f（x），当n≥2且x∈N*时，fn（x）=f（fn-1（x）），对于函数f（x）定义域内的x0，若正在正整数n是使得fn（x0）=x0成立的最小正整数，则称n是点x0的最小正周期，x0称为f（x）的n～周期点，已知定义在[0，1]上的函数f（x）的图象如图，对于函数f（x），下列说法正确的是①②③（写出所有正确命题的编号）
19．某中学为了解初三年级学生“掷实心球”项目的整体情况，随机抽取男、女生各20名进行测试，记录的数据如下：
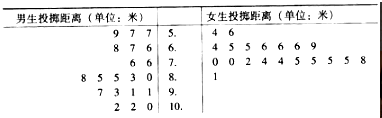
已知该项目评分标准为：
注：满分10分，且得9分以上（含9分）定为“优秀”．
（Ⅰ）求上述20名女生得分的中位数和众数；
（Ⅱ）从上述20名男生中，随机抽取2名，求抽取的2名男生中优秀人数X的分布列；
（Ⅲ）根据以上样本数据和你所学的统计知识，试估计该年级学生实心球项目的整体情况．（写出两个结论即可）
已知该项目评分标准为：
| 男生投掷距离（米） | … | [5.4，6.0） | [6.0，6.6） | [6.6，7.4） | [7.4，7.8） | [7.8，8.6） | [8.6，10.0） | [10.0，+∞） |
| 女生投掷距离（米） | … | [5.1，5.4） | [5.4，5.6） | [5.6，6.4） | [6.4，6.8） | [6.8，7.2） | [7.2，7.6） | [7.6，+∞） |
| 个人得分（分） | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
（Ⅰ）求上述20名女生得分的中位数和众数；
（Ⅱ）从上述20名男生中，随机抽取2名，求抽取的2名男生中优秀人数X的分布列；
（Ⅲ）根据以上样本数据和你所学的统计知识，试估计该年级学生实心球项目的整体情况．（写出两个结论即可）