题目内容
4.一袋中装有分别标记着1,2,3数字的3个小球,每次从袋中取出一个球(每只小球被取到的可能性相同),现连续取2次球,若每次取出一个球后放回袋中,记2次取出的球中标号最小的数字与最大的数字分别为X,Y,设ξ=Y-X,则Eξ=( )| A. | $\frac{4}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{8}{9}$ | D. | 1 |
分析 由ξ=0,1,2,可得P(ξ=0)=$\frac{{C}_{3}^{1}}{9}$,P(ξ=1)=$\frac{2+2}{9}$,P(ξ=2)=$\frac{2}{9}$,即可得出E(ξ).
解答 解:∵ξ=0,1,2,P(ξ=0)=$\frac{{C}_{3}^{1}}{9}$=$\frac{1}{3}$,P(ξ=1)=$\frac{2+2}{9}$=$\frac{4}{9}$,P(ξ=2)=$\frac{2}{9}$,
∴E(ξ)=0×$\frac{1}{3}+1×\frac{4}{9}$+2×$\frac{2}{9}$=$\frac{8}{9}$,
故选:C.
点评 本题考查了古典概率计算公式及其数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
19.某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下:
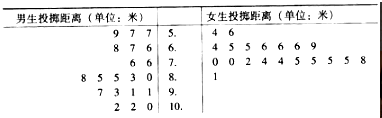
已知该项目评分标准为:
注:满分10分,且得9分以上(含9分)定为“优秀”.
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)

已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)
13.已知正三棱锥P-ABC中E,F分别是AC,PC的中点,若EF⊥BF,AB=2,则三棱锥P-ABC的外接球的表面积( )
| A. | 4π | B. | 6π | C. | 8π | D. | 12π |
14.某工厂加工某种零件的三道供需流程图如图所示,则该种零件可导致废品的环节有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 定义:f1(x)=f(x),当n≥2且x∈N*时,fn(x)=f(fn-1(x)),对于函数f(x)定义域内的x0,若正在正整数n是使得fn(x0)=x0成立的最小正整数,则称n是点x0的最小正周期,x0称为f(x)的n~周期点,已知定义在[0,1]上的函数f(x)的图象如图,对于函数f(x),下列说法正确的是①②③(写出所有正确命题的编号)
定义:f1(x)=f(x),当n≥2且x∈N*时,fn(x)=f(fn-1(x)),对于函数f(x)定义域内的x0,若正在正整数n是使得fn(x0)=x0成立的最小正整数,则称n是点x0的最小正周期,x0称为f(x)的n~周期点,已知定义在[0,1]上的函数f(x)的图象如图,对于函数f(x),下列说法正确的是①②③(写出所有正确命题的编号)