题目内容
已知正实数a,b满足
+
=3,则(a+1)(b+2)的最小值是 .
| 1 |
| a |
| 2 |
| b |
考点:基本不等式
专题:不等式的解法及应用
分析:正实数a,b满足
+
=3,可得3≥2
,b+2a=3ab.展开(a+1)(b+2)=ab+b+2a+2=4ab+2,即可得出.
| 1 |
| a |
| 2 |
| b |
|
解答:
解:∵正实数a,b满足
+
=3,
∴3≥2
,化为ab≥
,当且仅当b=2a=
时取等号.
b+2a=3ab.
∴(a+1)(b+2)=ab+b+2a+2=4ab+2≥
+2=
.
故答案为:
.
| 1 |
| a |
| 2 |
| b |
∴3≥2
|
| 8 |
| 9 |
| 4 |
| 3 |
b+2a=3ab.
∴(a+1)(b+2)=ab+b+2a+2=4ab+2≥
| 32 |
| 9 |
| 50 |
| 9 |
故答案为:
| 50 |
| 9 |
点评:本题考查了基本不等式的性质,考查了计算能力,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=logax(0<a<1)的导函数f′(x),A=f′(a),b=f(a+1)-f(a),C=f′(a+1),D=f(a+2)-f(a+1),则A,B,C,D中最大的数是( )
| A、A | B、B | C、C | D、D |
将“你能HOlD住吗”8个汉字及英文字母填人5×4的方格内,其中“你”字填入左上角,“吗”字填入右下角,将其余6个汉字及英文字母依次填入方格,要求只能横读或竖读成一句原语,如图所示为一种填法,则共有不同的填法种数是( )
| 你 | 能 | |||
| H | O | |||
| L | D | 住 | ||
| 吗 |
| A、35 | B、15 | C、20 | D、70 |
已知点A(-1,0,1),B(2,4,3),C(5,8,5),则( )
| A、三点构成等腰三角形 |
| B、三点构成直角三角形 |
| C、三点构成等腰直角三角形 |
| D、三点不能构成三角形 |
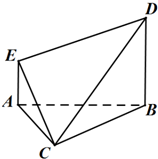 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1.
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1.