题目内容
16.由区域$\left\{\begin{array}{l}{y≤2x}\\{x+2y-4≥0}\\{x+y-4≤0}\end{array}\right.$中的点在直线ax+by+c=0(a,b,c∈R)上的投影构成的线段记为AB,则|AB|的最小值为$\frac{4\sqrt{2}}{5}$.分析 作出不等式组对应的平面区域,利用投影的定义,利用数形结合进行求解即可.
解答 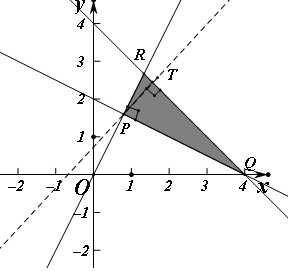 解:作出不等式组对应的平面区域如图:(阴影部分),
解:作出不等式组对应的平面区域如图:(阴影部分),
三条直线的交点分别为P($\frac{4}{5},\frac{8}{5}$),Q(4,0),R($\frac{4}{3},\frac{8}{3}$),因为PQ⊥PR,可行域为Rt△PQR,作斜边RQ的高PT,求值PQ=$\frac{8}{\sqrt{5}}$,PR=$\frac{8}{3\sqrt{5}}$,RQ=$\frac{8\sqrt{2}}{3}$,
所以当直线ax+by+c=0(a,b,c∈R)与PT平行时,区域中的点在直线上的投影构成的线段记为AB最小,
则|AB|的最小值为$\frac{PQ•PR}{RQ}=\frac{4\sqrt{2}}{5}$;
故答案为:$\frac{4\sqrt{2}}{5}$.
点评 本题考查了简单线性规划问题;关键是明确直线ax+by+c=0(a,b,c∈R)上的投影构成的线段AB最小值时直线的位置.运用了数形结合的思想.

练习册系列答案
相关题目
6.i为虚数单位,则(${\frac{1-i}{1+i}}$)2017=( )
| A. | -i | B. | -1 | C. | i | D. | 1 |
1.设f(x)=cos2x-sin2x,把y=f(x)的图象向右平移φ(φ>0)个单位后,恰好得到函数y=f(x)的图象,则φ的值可以为( )
| A. | $\frac{π}{2}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{3π}{2}$ |
8.已知函数f(x)是偶函数,f(x+1)是奇函数,且对任意的x1,x2∈[0,1],且x1≠x2,都有(x1-x2)[f(x1)-f(x2)]<0,设a=f($\frac{82}{11}$),b=-f($\frac{50}{9}$),c=f($\frac{24}{7}$),则下列结论正确的是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>a>b |
5.函数f(x)=sin(ωx+φ)+$\sqrt{3}cos({ωx+φ})({ω>0})$的图象过(1,2),若f(x)相邻的零点为x1,x2且满足|x1-x2|=6,则f(x)的单调增区间为( )
| A. | [-2+12k,4+12k](k∈Z) | B. | [-5+12k,1+12k](k∈Z) | C. | [1+12k,7+12k](k∈Z) | D. | [-2+6k,1+6k](k∈Z) |
6.若存在正实数m,使得关于x的方程x+a(2x+2m-4ex)[ln(x+m)-lnx]=0成立,其中e为自然对数的底数,则实数a的取值范围是( )
| A. | (-∞,0) | B. | $(0,\frac{1}{2e})$ | C. | $(-∞,0)∪[\frac{1}{2e},+∞)$ | D. | $[\frac{1}{2e},+∞)$ |
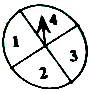 在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯n关时,转n次,当次转得数字之和大于n2时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍.假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.
在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯n关时,转n次,当次转得数字之和大于n2时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍.假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.