题目内容
11.若a>0,b>0,a+b=$\frac{1}{a}$+$\frac{1}{b}$,则3a+81b的最小值为( )| A. | 6 | B. | 9 | C. | 18 | D. | 24 |
分析 a>0,b>0,a+b=$\frac{1}{a}$+$\frac{1}{b}$,化为ab(a+b)=a+b>0,可得ab=1.再利用基本不等式的性质即可得出.
解答 解:∵a>0,b>0,a+b=$\frac{1}{a}$+$\frac{1}{b}$,∴ab(a+b)=a+b>0,∴ab=1.
则3a+81b≥2$\sqrt{{3}^{a}•{3}^{4b}}$=2$\sqrt{{3}^{a+4b}}$≥2$\sqrt{{3}^{2\sqrt{a•4b}}}$=18,当且仅当a=4b=2时取等号.
∴3a+81b的最小值为18.
故选:C.
点评 本题考查了指数函数的运算法则、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.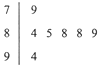 如图是2015年日喀则市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字.这些数据的中位数是______,去掉一个最低分和最高分后所剩数据的平均数是( )
如图是2015年日喀则市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字.这些数据的中位数是______,去掉一个最低分和最高分后所剩数据的平均数是( )
 如图是2015年日喀则市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字.这些数据的中位数是______,去掉一个最低分和最高分后所剩数据的平均数是( )
如图是2015年日喀则市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字.这些数据的中位数是______,去掉一个最低分和最高分后所剩数据的平均数是( )| A. | 86.5; 86.7 | B. | 88; 86.7 | C. | 88;86.8 | D. | 86.5;86.8 |
6.复数$\frac{5i}{{2+{i^9}}}$的共轭复数所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.设复数z=2+i,若复数$z+\frac{1}{z}$的虚部为b,则b等于( )
| A. | $\frac{4}{5}$ | B. | $\frac{4}{5}i$ | C. | $\frac{6}{5}$ | D. | $\frac{6}{5}i$ |
20.平面直角坐标系中,已知O为坐标原点,点A、B的坐标分别为(1,1)、(-3,3).若动点P满足$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,其中λ、μ∈R,且λ+μ=1,则点P的轨迹方程为( )
| A. | x-y=0 | B. | x+y=0 | C. | x+2y-3=0 | D. | (x+1)2+(y-2)2=5 |
1.《九章算术》是我国古代数学名著,也是古代东方数学的代表作.书中有如下问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“已知直角三角形两直角边长分别为5步和12步,问其内接正方形边长为多少步?”现若向此三角形内投豆子,则落在其内接正方形内的概率是( )
| A. | $\frac{60}{289}$ | B. | $\frac{90}{289}$ | C. | $\frac{120}{289}$ | D. | $\frac{240}{289}$ |