题目内容
已知函数f（x）=3x+1，x∈[-1，5]，且f（x）≥c+1，求c的取值范围．
考点：一次函数的性质与图象
专题：函数的性质及应用
分析：求出函数f（x）的最小值即可得到结论．
解答：
解：∵函数f（x）=3x+1，x∈[-1，5]，
∴-2≤f（x）≤16，
要使且f（x）≥c+1成立，
则c+1≤-2，即且c≤-3，
故c的取值范围是（-∞，-3]．
∴-2≤f（x）≤16，
要使且f（x）≥c+1成立，
则c+1≤-2，即且c≤-3，
故c的取值范围是（-∞，-3]．
点评：本题主要考查函数值域的应用，根据一次函数的性质求出函数的值域是解决本题的关键．
练习册系列答案
相关题目
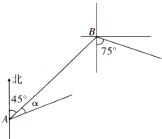在一次海上联合作战演习中，红方一艘侦察艇发现在北偏东45°方向，相距12n mile的水面上，有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进，若侦察艇以每小时14n mile的速度，沿北偏东45°+α方向拦截蓝方的小艇，若要在最短的时间内拦截住，求红方侦察艇所需的时间和角α的正弦值．（注：n mile是海里的英文符号）