题目内容
16.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,O为坐标原点,点P(1,$\frac{\sqrt{2}}{2}$)在椭圆上,连接PF1交y轴于点Q,点Q满足$\overrightarrow{PQ}$=$\overrightarrow{Q{F}_{1}}$.直线l不过原点O且不平行于坐标轴,l与椭圆C有两个交点A,B.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点M($\frac{5}{4}$,0),若直线l过椭圆C的右焦点F2,证明:$\overrightarrow{MA}$•$\overrightarrow{MB}$为定值;
(Ⅲ)若直线l过点(0,2),设N为椭圆C上一点,且满足$\overrightarrow{OA}$+$\overrightarrow{OB}$=λ$\overrightarrow{ON}$,求实数λ的取值范围.
分析 (Ⅰ)由题意可知:c=1,$\frac{{b}^{2}}{a}$=$\frac{\sqrt{2}}{2}$,a2=b2-c2,即可求得a和b的值,求得椭圆方程;
(Ⅱ)设直线AB的方程,代入椭圆方程,由韦达定理定理及向量数量积的坐标运算,即可求证$\overrightarrow{MA}$•$\overrightarrow{MB}$为定值;
(Ⅲ)分类讨论,设直线AB的方程,代入椭圆方程,由△>0,求得k2>$\frac{3}{2}$,由韦达定理,向量数量积的坐标运算,即可求得4=$\frac{{λ}^{2}}{4}$(1+2k2),即可求得实数λ的取值范围.
解答 解:(Ⅰ)由$\overrightarrow{PQ}$=$\overrightarrow{Q{F}_{1}}$,则Q为PF1的中点,则PF1⊥F1F2,
则c=1,$\frac{{b}^{2}}{a}$=$\frac{\sqrt{2}}{2}$,a2=b2-c2,
解得:a=$\sqrt{2}$,b=1,
∴椭圆的标准方程:$\frac{{x}^{2}}{2}+{y}^{2}=1$;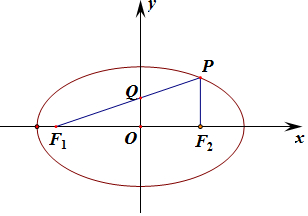
(Ⅱ)证明:由题意可知:设直线l的方程y=k(x-1),k≠1,设A(x1,y1),B(x2,y2),
∴$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:(1+2k2)x2-4k2x+2k2-2=0,
则x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$,y1y2=k2(x1-1)(x2-1)=k2x1x2-k2(x1+x2)+k2,
由$\overrightarrow{MA}$=(x1-$\frac{5}{4}$,y1),$\overrightarrow{MB}$=(x2-$\frac{5}{4}$,y2),
则$\overrightarrow{MA}$•$\overrightarrow{MB}$=(x1-$\frac{5}{4}$,y1)(x2-$\frac{5}{4}$,y2)=(1+k2)x1x2-(k2+$\frac{5}{4}$)(x1+x2)+$\frac{25}{16}$+k2,
=(1+k2)×$\frac{2{k}^{2}-2}{1+2{k}^{2}}$-(k2+$\frac{5}{4}$)×$\frac{4{k}^{2}}{1+2{k}^{2}}$+$\frac{25}{16}$+k2,
=$\frac{-2(1+2{k}^{2})}{1+2{k}^{2}}$$\frac{25}{16}$+$\frac{25}{16}$,
=-$\frac{7}{16}$,
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$为定值,定值为-$\frac{7}{16}$;
(Ⅲ)设A(x1,y1),B(x2,y2),Q(x0,y0).
当λ=0时,由$\overrightarrow{OA}$+$\overrightarrow{OB}$=λ$\overrightarrow{ON}$,$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{0}$,A与B关于原点对称,存在Q满足题意,
∴λ=0成立;
当λ≠0时,联立$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得(1+2k2)x2+8kx+6=0,
由△=(8k)2-4×6(1+2k2)>0,解得k2>$\frac{3}{2}$,…(*),
∴x1+x2=-$\frac{8k}{1+2{k}^{2}}$,x1x2=$\frac{6}{1+2{k}^{2}}$,
y1+y2=k(x1+x2)+4=$\frac{4}{1+2{k}^{2}}$.
由$\overrightarrow{OA}$+$\overrightarrow{OB}$=λ$\overrightarrow{ON}$,得(x1+x2,y1+y2)=(λx0,λy0),可得x1+x2=λx0,y1+y2=λy0,
$\left\{\begin{array}{l}{{x}_{0}=\frac{1}{λ}({x}_{1}+{x}_{2})=-\frac{8k}{λ(1+2{k}^{2})}}\\{{y}_{0}=\frac{1}{λ}({y}_{1}+{y}_{2})=\frac{4}{λ(1+2{k}^{2})}}\end{array}\right.$,由Q在椭圆$\frac{{x}^{2}}{2}+{y}^{2}=1$上,
代入,整理得4=$\frac{{λ}^{2}}{4}$(1+2k2),
代入(*)式,得λ2<4,解得-2<λ<2且λ≠0.
综上可知:λ∈(-2,2).
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $4+log_2^6$ | B. | 4 | C. | $3+log_2^3$ | D. | $4+log_2^3$ |
①已知p3+q3=2,求证p+q≤2,用反证法证明时,可假设p+q≥2;
②已知a,b∈R,|a|+|b|<1,求证方程x2+ax+b=0的两根的绝对值都小于1,用反证法证明时可假设方程有一根x1的绝对值大于或等于1,即假设|x1|≥1.
下列说法中正确的是( )
| A. | ①与②的假设都错误 | B. | ①与②的假设都正确 | ||
| C. | ①的假设正确;②的假设错误 | D. | ①的假设错误;②的假设正确 |