题目内容
已知三棱锥的三视图如图所示，则它的外接球的表面积为（ ）
| A、4π | B、8π |
| C、12π | D、16π |
考点：球的体积和表面积,由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中三棱锥的三视图，我们可以求出三棱棱的高，即顶点到底面的距离，及底面外接圆的半径，进而求出三棱锥外接球的半径，代入球的表面积公式，即可求出外接球的表面积．
解答：
解：由已知中三棱锥的高为1
底面为一个直角三角形，
由于底面斜边上的中线长为1，
则底面的外接圆半径为1，
顶点在底面上的投影落在底面外接圆的圆心上，
由于顶点到底面的距离，与底面外接圆的半径相等
则三棱锥的外接球半径R为1，
则三棱锥的外接球表面积S=4πR2=4π
故选：A
底面为一个直角三角形，
由于底面斜边上的中线长为1，
则底面的外接圆半径为1，
顶点在底面上的投影落在底面外接圆的圆心上，
由于顶点到底面的距离，与底面外接圆的半径相等
则三棱锥的外接球半径R为1，
则三棱锥的外接球表面积S=4πR2=4π
故选：A
点评：本题考查的知识点是由三视图求表面积，其中根据三视图出判断出三棱锥的几何特征，进而求出其外接球的半径是解答本题的关键．
练习册系列答案
相关题目
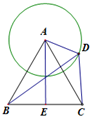△ABC是边长为2的等边三角形，D是以A为圆心，半径为1的圆上任意一点，如图所示，则| BD |
| CD |
A、3+
| ||
B、3-
| ||
C、3-2
| ||
D、3+2
|
已知x，y的取值如表所示，若y与x线性相关，且
=0.85x+a，则a=（ ）
 |
| y |
| x | 0 | 1 | 3 | 4 |
| y | 2.4 | 3.9 | 5.6 | 6.1 |
| A、2.2 | B、2.6 |
| C、2.8 | D、2.9 |
已知关于x的不等式
＜1的解集为{x|x＜1或x＞3}，则a的值为（ ）
| ax |
| x-1 |
| A、3 | ||
B、
| ||
C、-
| ||
D、
|