题目内容
证明f（x）=
在（-1，1）上为减函数．
|
考点：函数单调性的判断与证明
专题：证明题
分析：利用函数单调性的定义加以证明即可．
解答：
证明：设任意的x1，x2∈（-1，1），且x1＜x2，则
=
，
又（1-x1）（1+x2）-（1+x1）（1-x2）=2（x2-x1），
∵x1＜x2′，∴x2-x1＞0，
即（1-x1）（1+x2）＞（1+x1）（1-x2）=2，
∴
=＞1，即f（x1）＞f（x2），
∴f（x）=
在（-1，1）上为减函数．
| f(x1) |
| f(x2) |
|
又（1-x1）（1+x2）-（1+x1）（1-x2）=2（x2-x1），
∵x1＜x2′，∴x2-x1＞0，
即（1-x1）（1+x2）＞（1+x1）（1-x2）=2，
∴
| f(x1) |
| f(x2) |
∴f（x）=
|
点评：本题主要考查函数单调性的证明，采用作商法比较f（X1）与f（X2）的大小效果较好，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
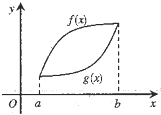已知函数f（x）和g（x）在区间[a，b]上的图象如图所示，那么下列说法正确的是（ ）| A、f（x）在a到b之间的平均变化率大于g（x）在a到b之间的平均变化率 |
| B、f（x）在a到b之间的平均变化率小于g（x）在a到b之间的平均变化率 |
| C、对于任意x0∈（a，b），函数f（x）在x=x0处的瞬时变化率总大于函数g（x）在x=x0处的瞬时变化率 |
| D、存在x0∈（a，b），使得函数f（x）在x=x0处的瞬时变化率小于函数g（x）在x=x0处的瞬时变化率 |
