题目内容
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
(Ⅰ)根据上面的频率分布表,估计该居民区PM2.5的24小时平均浓度超过50微克/立方米的概率;
(Ⅱ)计算样本众数、中位数和平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100) | 2 | 0.1 |
| 合计 | 20 | 1 |
(Ⅱ)计算样本众数、中位数和平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
考点:众数、中位数、平均数,频率分布直方图,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)利用频率分布表,能估计该居民区PM2.5的24小时平均浓度超过50微克/立方米的概率.
(Ⅱ)利用频率分布表,能求出样本众数、中位数、平均数,由此能判断该居民区的环境是否需要改进.
(Ⅱ)利用频率分布表,能求出样本众数、中位数、平均数,由此能判断该居民区的环境是否需要改进.
解答:
解:(Ⅰ)由已知共监测了20天,
用频率估计相应的概率p=0.15+0.1=0.25.…(3分)
(Ⅱ)样本众数约为37.5(微克/立方米),…(5分)
中位数约为37.5(微克/立方米),…(7分)
平均值约12.5×0.25+37.5×0.5+62.5×0.15+87.5×0.1=40(微克/立方米)…(10分)
∴去年该居民区PM2.5年平均浓度为:40(微克/立方米).
∵40>35,∴去年该居民区PM2.5年平均浓度不符合环境空气质量标准,
∴该居民区的环境需要改进.…(12分)
用频率估计相应的概率p=0.15+0.1=0.25.…(3分)
(Ⅱ)样本众数约为37.5(微克/立方米),…(5分)
中位数约为37.5(微克/立方米),…(7分)
平均值约12.5×0.25+37.5×0.5+62.5×0.15+87.5×0.1=40(微克/立方米)…(10分)
∴去年该居民区PM2.5年平均浓度为:40(微克/立方米).
∵40>35,∴去年该居民区PM2.5年平均浓度不符合环境空气质量标准,
∴该居民区的环境需要改进.…(12分)
点评:本题考查频率分布表的应用,是基础题,解题时要认真审题,注意读表识图能力的培养.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
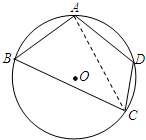 某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,
某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,