题目内容
在平面直角坐标系中，O为原点，A（0，sinα），B（2cosα，0），动点C满足|
|=1，则|
+
+
|的最大值是 ．
| AC |
| OA |
| OB |
| OC |
考点：向量在几何中的应用
专题：平面向量及应用
分析：由于动点C满足|
|=1，所以C在以A（0，sinα）为圆心的单位圆上，故设C（cosθ，sinθ+sinα），利用向量模的平方等于向量的平方，将|
+
+
|2=写成关于θ的三角函数解析式，利用余弦函数的有界性求最值．
| AC |
| OA |
| OB |
| OC |
解答：
解：∵|
|=1，
∴C在以A（0，sinα）为圆心的单位圆上，故设C（cosθ，sinθ+sinα），
∴|
+
+
|2=（2cosα+cosθ）2+（sinα+sinθ+sinα）2=sin2θ+cos2θ+4cosαcosθ+4sinαsinθ+4=4cos（α-θ）+5≤9
∴原式最大值3；
故答案为：3．
| AC |
∴C在以A（0，sinα）为圆心的单位圆上，故设C（cosθ，sinθ+sinα），
∴|
| OA |
| OB |
| OC |
∴原式最大值3；
故答案为：3．
点评：本题考查了向量的模与向量的平方相等以及利用三角函数的有界性求最值，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC内接于⊙O于A，AD切⊙O于A，∠BAD=60°，则∠ACB=（ ）
| A、120° | B、150° |
| C、90° | D、100° |
若以点F1（-2，0）、F2（2，0）为焦点的双曲线C过直线l：x+y-1=0上一点M，则能使所作双曲线C的实轴长最长时的双曲线方程为（ ）
A、x2-
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
对?x1，x2∈（0，
），若x2＞x1，且y1=
，y2=
，则（ ）
| π |
| 2 |
| 1+sinx1 |
| x1 |
| 1+sinx2 |
| x2 |
| A、y1=y2 |
| B、y1＞y2 |
| C、y1＜y2 |
| D、y1，y2的大小关系不能确定 |
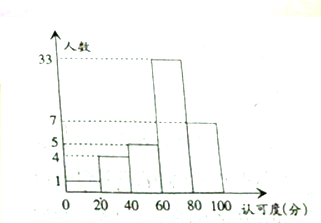某校为了了解新的一轮教改模式有效性的“认可度”，在全校师生（可认为很多人）进行了“认可度”的问卷调查，现随机抽查50名师生，对他们的“认可度”统计分析得如图