题目内容
20.正态分布密度函数Φ(x)=$\frac{1}{\sqrt{2π}•σ}•{e}^{{-}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}}$其中μ<0,的图象可能为( )| A. | 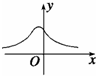 | B. |  | C. | 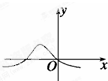 | D. |  |
分析 由函数表达式Φ(x)=$\frac{1}{\sqrt{2π}•σ}•{e}^{{-}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}}$判断函数的性质,从而解得.
解答 解:易知Φ(x)=$\frac{1}{\sqrt{2π}•σ}•{e}^{{-}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}}$>0恒成立,
故排除C,
又∵Φ(x)=$\frac{1}{\sqrt{2π}•σ}•{e}^{{-}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}}$的图象关于x=u对称,
故排除B,D;
故选A.
点评 本题考查了函数的性质的判断与应用及数形结合的思想应用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
11.“x=1”是“x2-x=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知曲线C:$\frac{x|x|}{{a}^{2}}$-$\frac{y|y|}{{b}^{2}}$=1(a>b>0),下列叙述中正确的是( )
| A. | 垂直于x轴的直线与曲线C存在两个交点 | |
| B. | 直线y=kx+m(k,m∈R)与曲线C最多有三个交点 | |
| C. | 曲线C关于直线y=-x对称 | |
| D. | 若P1(x1,y1),P2(x2,y2)为曲线C上任意两点,则有$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$<0 |
9.自变量x0变到x1(x1>x0)时,函数值的增量与相应自变量的增量之比是函数( )
| A. | 在区间[x0,x1]上的平均变化率 | B. | 在x0处的变化率 | ||
| C. | 在x1处的变化量 | D. | 在区间[x0,x1]上的导数 |
10. 甲、乙两名同学在高考前的7次数学模拟测试中,四个填空题的成绩统计如图的茎叶图所示,则关于甲、乙两名同学的成绩分析不正确的是( )
甲、乙两名同学在高考前的7次数学模拟测试中,四个填空题的成绩统计如图的茎叶图所示,则关于甲、乙两名同学的成绩分析不正确的是( )
 甲、乙两名同学在高考前的7次数学模拟测试中,四个填空题的成绩统计如图的茎叶图所示,则关于甲、乙两名同学的成绩分析不正确的是( )
甲、乙两名同学在高考前的7次数学模拟测试中,四个填空题的成绩统计如图的茎叶图所示,则关于甲、乙两名同学的成绩分析不正确的是( )| A. | 甲、乙两位同学填空题的成绩的中位数都是15 | |
| B. | 甲同学填空题的成绩的众数是15 | |
| C. | 乙同学填空题的成绩的众数是20 | |
| D. | 乙同学填空题的平均成绩要好些 |