题目内容
9.自变量x0变到x1(x1>x0)时,函数值的增量与相应自变量的增量之比是函数( )| A. | 在区间[x0,x1]上的平均变化率 | B. | 在x0处的变化率 | ||
| C. | 在x1处的变化量 | D. | 在区间[x0,x1]上的导数 |
分析 函数的函数值从f(x0)改变到f(x1),改变量为f(x1)-f(x0),对应的自变量从x0改变到x1,改变量为x1-x0,函数改变量与自变量的改变量的比值成为函数在区间[x0,x1]上的平均变化率.
解答 解:当自变量由x0变化到x1时,自变量的“增量”为x1-x0,对应的函数值的“增量”为f(x1)-f(x0),
比值$\frac{f({x}_{1})-f({x}_{0})}{{x}_{1}-{x}_{0}}$为函数在区间[x0,x1]上的平均变化率.
故选A.
点评 本题考查了变化的快慢与变化率,是基础的概念题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.命题:“若x2<1,则-1<x<1”的逆否命题是( )
| A. | 若x≥1或 x≤-1,则 x2≥1 | B. | 若-1<x<1,则 x2<1 | ||
| C. | 若x>1或x<-1,则 x2>1 | D. | 若 x2≥1,则 x≥1或 x≤-1 |
20.正态分布密度函数Φ(x)=$\frac{1}{\sqrt{2π}•σ}•{e}^{{-}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}}$其中μ<0,的图象可能为( )
| A. | 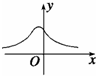 | B. |  | C. | 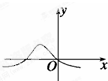 | D. |  |
14.已知实数a,b满足$\left\{{\begin{array}{l}{0<a<2}\\{0<b<2}\end{array}}\right.$,则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$表示焦点在x轴上且离心率小于$\frac{{\sqrt{3}}}{2}$的椭圆的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
1.某市一共有13个行政县,其中有5个贫困县,市教育局开学后准备从中抽取2个县进行调研,则抽到2个县都是贫困县的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{5}{39}$ |