题目内容
5.已知曲线C:$\frac{x|x|}{{a}^{2}}$-$\frac{y|y|}{{b}^{2}}$=1(a>b>0),下列叙述中正确的是( )| A. | 垂直于x轴的直线与曲线C存在两个交点 | |
| B. | 直线y=kx+m(k,m∈R)与曲线C最多有三个交点 | |
| C. | 曲线C关于直线y=-x对称 | |
| D. | 若P1(x1,y1),P2(x2,y2)为曲线C上任意两点,则有$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$<0 |
分析 对x,y的符号进行讨论,得出曲线的图象,根据椭圆与双曲线的性质进行判断.
解答 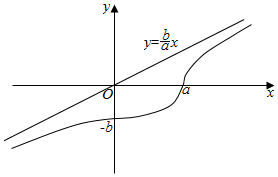 解:当x>0,y>0时,曲线C的方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$,渐近线方程为y=$\frac{b}{a}x$.
解:当x>0,y>0时,曲线C的方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$,渐近线方程为y=$\frac{b}{a}x$.
当x<0,y>0时,曲线C方程为-$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$,方程无解.
当x<0,y<0时,曲线C方程为$\frac{{y}^{2}}{{b}^{2}}-\frac{{x}^{2}}{{a}^{2}}=1$,渐近线方程为y=$\frac{b}{a}x$.
当x>0,y<0时,曲线C方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$.
作出曲线C的图象如图所示:
显然y是关于x的函数,故A错误.
由图象可知当直线y=kx+m经过点(a,0)且k>$\frac{b}{a}$时,直线与曲线C有三个交点.
∵a≠b,∴曲线C不关于直线y=-x对称,故C错误.
由图象可知y=f(x)为增函数,∴k${\;}_{{P}_{1}{P}_{2}}$=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$>0,故D错误.
综上,故选B.
点评 本题考查了曲线的方程的含义,椭圆与双曲线的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.正态分布密度函数Φ(x)=$\frac{1}{\sqrt{2π}•σ}•{e}^{{-}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}}$其中μ<0,的图象可能为( )
| A. | 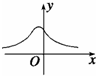 | B. |  | C. | 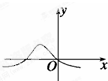 | D. |  |
10.我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架“歼-15”飞机准备着舰,如果甲机不能最先着舰,而乙机必须在丙机之前着舰(不一定相邻),那么不同的着舰方法种数为( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
14.已知实数a,b满足$\left\{{\begin{array}{l}{0<a<2}\\{0<b<2}\end{array}}\right.$,则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$表示焦点在x轴上且离心率小于$\frac{{\sqrt{3}}}{2}$的椭圆的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
15.已知函数f(x)=$\frac{x}{x+1}$+2x-mln(x+1)在(-1,+∞)上是增函数,则实数m的取值范围为( )
| A. | (-∞,2$\sqrt{2}$] | B. | (-∞,2$\sqrt{2}$) | C. | (-∞,3) | D. | (-∞,3] |