题目内容
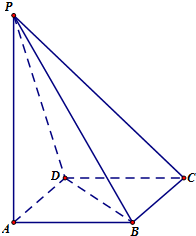 如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,
如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,(1)求证:BD⊥PC.
(2)若PA=2AB,∠BAD=45°,求PD与平面PAB所成角的正弦值.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明BD⊥平面PAC,利用直线与平面垂直的性质即可证得BD⊥PC;
(2)过D作DE⊥AB,垂足为E,连接PE,则DE⊥平面PAB,∠DPE是PD与平面PAB所成角,即可求解.
(2)过D作DE⊥AB,垂足为E,连接PE,则DE⊥平面PAB,∠DPE是PD与平面PAB所成角,即可求解.
解答:
 (1)证明:∵PA⊥底面ABCD,BD?底面ABCD,
(1)证明:∵PA⊥底面ABCD,BD?底面ABCD,
∴PA⊥BD;①
又底面ABCD是菱形,
∴AC⊥BD;②
PA∩AC=A,
∴BD⊥平面PAC,PC?平面PAC,
∴BD⊥PC;
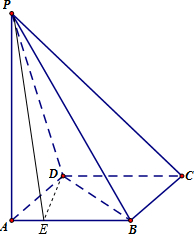
(2)解:过D作DE⊥AB,垂足为E,连接PE,则DE⊥平面PAB,
∴∠DPE是PD与平面PAB所成角,
设DE=1,则AD=
,PA=2
,
∴PD=
=
,
∴sin∠DPE=
=
.
 (1)证明:∵PA⊥底面ABCD,BD?底面ABCD,
(1)证明:∵PA⊥底面ABCD,BD?底面ABCD,∴PA⊥BD;①
又底面ABCD是菱形,
∴AC⊥BD;②
PA∩AC=A,
∴BD⊥平面PAC,PC?平面PAC,
∴BD⊥PC;
(2)解:过D作DE⊥AB,垂足为E,连接PE,则DE⊥平面PAB,
∴∠DPE是PD与平面PAB所成角,
设DE=1,则AD=
| 2 |
| 2 |
∴PD=
| 2+8 |
| 10 |
∴sin∠DPE=
| DE |
| PD |
| ||
| 10 |
点评:本题考查的知识点是直线与平面所成的角,直线与平面垂直的判定与性质,熟练掌握线面垂直与平行的判定定理和性质定理是解题的关键.属于中档题.

练习册系列答案
相关题目

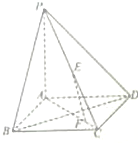 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.