题目内容
若函数f(x)定义域为R,取x0∈R并且xn+1=f(xn)(n∈N),则称{xn}是f(x)的迭代数列.已知{an},{bn}均是f(x)=
的迭代数列,Sn=
ak,Tn=
bk.
(Ⅰ)对任意x,y∈R且x≠y,求证:|f(x)-f(y)|<
|x-y|.
(Ⅱ)求证:|Sn-Tn|<
(n∈N+).
(Ⅲ)求证:存在唯一实数T满足|Sn-nt|<
(n∈N+).
| 1 |
| x2+2 |
| n |
 |
| k=1 |
| n |
 |
| k=1 |
(Ⅰ)对任意x,y∈R且x≠y,求证:|f(x)-f(y)|<
| 1 |
| 4 |
(Ⅱ)求证:|Sn-Tn|<
| 2 |
| 3 |
(Ⅲ)求证:存在唯一实数T满足|Sn-nt|<
| 2 |
| 3 |
考点:数列与函数的综合,数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件得|f(x)-f(y)|=
|x-y|≤
•|x-y|,从而得到
<
,由此能证明|f(x)-f(y)|<
|x-y|.
(Ⅱ)由(Ⅰ)知|ak-bk|≤
|ak-1-bk-1|≤…≤(
)k-1|a1-b1|,从而得到|ak-bk|<
(
)k-1对任意正整数k成立,由此能证明|Sn-Tn |<
.
(Ⅲ)由已知条件推导出|at-t|=≤
|ak-t-t|,从而昨到|ak-t|<
•(
)k-1对任意正整数k成立,由此能证明存在唯一实数T满足|Sn-nt|<
(n∈N+).
| |x+y| |
| (x2+2)(y2+2) |
| |x|+|y| |
| (x2+2)(y2+2) |
| |x|+|y| |
| (x2+2)(y2+2) |
| 1 |
| 4 |
| 1 |
| 4 |
(Ⅱ)由(Ⅰ)知|ak-bk|≤
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
(Ⅲ)由已知条件推导出|at-t|=≤
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
解答:
(Ⅰ)证明:∵f(x)=
,
∴|f(x)-f(y)|=
|x-y|≤
•|x-y|,
-
=
,
∴
<
,又∵x≠y,
∴|f(x)-f(y)|<
|x-y|.…(4分)
(Ⅱ)由第(Ⅰ)题结论知:|ak-bk|≤
|ak-1-bk-1|≤…≤(
)k-1|a1-b1|,
∵a1=f(a0),b1=f(b0),
∴0<x1≤
,0<b1 ≤
,∴|a1-b1|<
,
∴|ak-bk|<
(
)k-1对任意正整数k成立,
∴|Sn-Tn |=|
(ak-bk)|≤
|ak-yk|
<
(
)k-1=
-
(
)n<
,(n∈N* ).…(8分)
(Ⅲ)证明:记F(x)=f(x)-x,F(0)>0,F(1)<0,
∴F(x)存在零点x=t,
即t=f(t),由第(1)题结论知:|at-t|=|f(ak-1)-f(t)|≤
|ak-t-t|,
∴|ak-t|≤
|ak-1-t|≤…≤(
)k-1|a1-t|,
∵a1 =f(a0),t=f(t),0<a1≤
,0<t<
,
∴|a1-t|<
,∴|ak-t|<
•(
)k-1对任意正整数k成立,
|Sn-nt|=|
(ak -t)|
≤
|ak-t|<
(
)t-1=
-
(
)n<
,(n∈N*),
假设还存在另一个实数t′ 满足|Sn-nt′|<
,(n∈N*),
∴|t-t′|=
|nt-Sn+Sn-nt′|<
对任意正整数n成立,
∴|t-t′|≤0,即t=t′,这与t≠t′相矛盾,
∴符合题意的实数t存在且唯一.…(13分)
| 1 |
| x2+2 |
∴|f(x)-f(y)|=
| |x+y| |
| (x2+2)(y2+2) |
| |x|+|y| |
| (x2+2)(y2+2) |
| 1 |
| 4 |
| |x|+|y| |
| (x2+2)(y2+2) |
| x2y2+2(|x|-1)2+2(|x|-1)2 |
| 4(x2+2)(y2+2) |
∴
| |x|+|y| |
| (x2+2)(y2+2) |
| 1 |
| 4 |
∴|f(x)-f(y)|<
| 1 |
| 4 |
(Ⅱ)由第(Ⅰ)题结论知:|ak-bk|≤
| 1 |
| 4 |
| 1 |
| 4 |
∵a1=f(a0),b1=f(b0),
∴0<x1≤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴|ak-bk|<
| 1 |
| 2 |
| 1 |
| 4 |
∴|Sn-Tn |=|
| n |
 |
| k=1 |
| n |
 |
| k=1 |
<
| n |
 |
| k=1 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
(Ⅲ)证明:记F(x)=f(x)-x,F(0)>0,F(1)<0,
∴F(x)存在零点x=t,
即t=f(t),由第(1)题结论知:|at-t|=|f(ak-1)-f(t)|≤
| 1 |
| 4 |
∴|ak-t|≤
| 1 |
| 4 |
| 1 |
| 4 |
∵a1 =f(a0),t=f(t),0<a1≤
| 1 |
| 2 |
| 1 |
| 2 |
∴|a1-t|<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
|Sn-nt|=|
| n |
 |
| k=1 |
≤
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
假设还存在另一个实数t′ 满足|Sn-nt′|<
| 2 |
| 3 |
∴|t-t′|=
| 1 |
| n |
| 4 |
| 3n |
∴|t-t′|≤0,即t=t′,这与t≠t′相矛盾,
∴符合题意的实数t存在且唯一.…(13分)
点评:本题考查不等式的证明,考查符合条件的实数唯一存在的证明,解题时要认真审题,注意数列与函数的综合运用.

练习册系列答案
相关题目
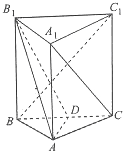 在三棱柱ABC-A1B1C1中,已知平面BB1C1C⊥平面ABC,AB=AC,D是BC中点,且B1D⊥BC1.
在三棱柱ABC-A1B1C1中,已知平面BB1C1C⊥平面ABC,AB=AC,D是BC中点,且B1D⊥BC1.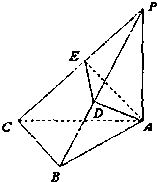 如图,PA⊥平面ABC,AB⊥BC.AD垂直于PB于D,AE垂直于PC于E.PA=
如图,PA⊥平面ABC,AB⊥BC.AD垂直于PB于D,AE垂直于PC于E.PA=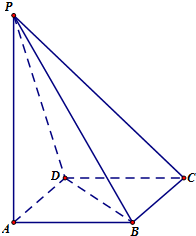 如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,
如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,