题目内容
设
，
是两个不共线向量，已知
=2
+k
，
=
+3
，
=2
-
．
（1）若A，B，D三点共线，求实数k的值；
（2）若
，
为单位向量，
，
的夹角是
π，且
⊥
，求k的值．
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| CB |
| e1 |
| e2 |
| CD |
| e1 |
| e2 |
（1）若A，B，D三点共线，求实数k的值；
（2）若
| e1 |
| e2 |
| e1 |
| e2 |
| 2 |
| 3 |
| AB |
| CB |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：（1）三点共线问题可以转化为向量共线问题求解，利用共线向量定理的条件可以构建k的方程，解方程即可求出k的值；
（2）由
⊥
，可得
•
=0，结合
，
为单位向量，
，
的夹角是
π，可以构建关于k的方程，解方程可以求出k．
（2）由
| AB |
| CB |
| AB |
| CB |
| e1 |
| e2 |
| e1 |
| e2 |
| 2 |
| 3 |
解答：
解：（1）
=
-
=（2
-
）-（
+3
）=
1-4
2，
由A，B，D三点共线，根据共线向量定理的条件可得：
=λ
，2
+k
=λ（
1-4
2），
解得：k=-8．
∴A，B，D三点共线时实数k的值为-8．
（2）∵
⊥
，∴
•
=0
•
=（2
+k
）•（
+3
，）
=2+3k+（k+6）
1•
2
=2+3k+（k+6）cos
=
k-1=0
解得：k=
．
| BD |
| CD |
| CB |
| e1 |
| e2 |
| e1 |
| e2 |
| e |
| e |
由A，B，D三点共线，根据共线向量定理的条件可得：
| AB |
| BD |
| e1 |
| e2 |
| e |
| e |
解得：k=-8．
∴A，B，D三点共线时实数k的值为-8．
（2）∵
| AB |
| CB |
| AB |
| CB |
| AB |
| CB |
| e1 |
| e2 |
| e1 |
| e2 |
=2+3k+（k+6）
| e |
| e |
=2+3k+（k+6）cos
| 2π |
| 3 |
=
| 5 |
| 2 |
解得：k=
| 2 |
| 5 |
点评：本题考查了向量共线的条件及向量数量积的运算，解题的关键是利用条件构建方程，主要考查了方程思想．
练习册系列答案
相关题目
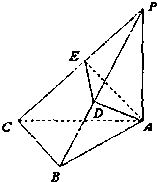如图，PA⊥平面ABC，AB⊥BC．AD垂直于PB于D，AE垂直于PC于E．PA=
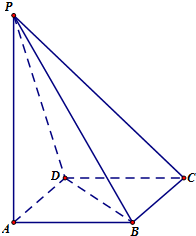如图在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，
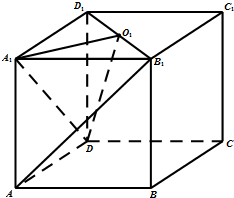已知长方体ABCD-A1B1C1D1，点O1为B1D1的中点．