题目内容
14.已知平面向量$\overrightarrow{a}$=($\sqrt{3}$,-1),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).(1)证明:$\overrightarrow{a}$⊥$\overrightarrow{b}$;
(2)若存在不同时为零的实数k和t,使$\overrightarrow{c}$=$\overrightarrow{a}$+(t2-3)$\overrightarrow{b}$,$\overrightarrow{d}$=-k$\overrightarrow{a}$+t$\overrightarrow{b}$,且$\overrightarrow{c}$⊥$\overrightarrow{d}$,试求函数关系式k=f(t).
分析 (1)计算$\overrightarrow{a}•\overrightarrow{b}$=0即可得出结论;
(2)令$\overrightarrow{c}$•$\overrightarrow{d}$=0即可得出k=f(t).
解答 (1)证明∵$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{3}$×$\frac{1}{2}$-1×$\frac{\sqrt{3}}{2}$=0,∴$\overrightarrow{a}⊥\overrightarrow{b}$.
(2)解:∵$\overrightarrow{c}$=$\overrightarrow{a}$+(t2-3)$\overrightarrow{b}$,$\overrightarrow{d}$=-k$\overrightarrow{a}$+t$\overrightarrow{b}$,且$\overrightarrow{c}⊥\overrightarrow{d}$,
∴$\overrightarrow{c}$•$\overrightarrow{d}$=[$\overrightarrow{a}$+(t2-3)$\overrightarrow{b}$]•(-k$\overrightarrow{a}$+t$\overrightarrow{b}$)
=-k${\overrightarrow{a}}^{2}$+t(t2-3)$\overrightarrow{b}$2+[t-k(t2-3)]$\overrightarrow{a}•\overrightarrow{b}$=0.
又$\overrightarrow{a}$2=|$\overrightarrow{a}$|2=4,$\overrightarrow{b}$2=|$\overrightarrow{b}$|2=1,$\overrightarrow{a}•\overrightarrow{b}$=0,
∴-4k+t3-3t=0,
∴k=f(t)=$\frac{{t}^{3}-3t}{4}$(t≠0).
点评 本题考查了平面向量的数量积运算,向量垂直与数量积的关系,属于中档题.

| A. | $\frac{85}{225}$ | B. | $\frac{86}{225}$ | C. | $\frac{88}{225}$ | D. | $\frac{89}{225}$ |
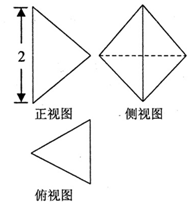 某几何体的三视图如图所示,其俯视图是边长为1的正三角形,侧视图是菱形,则这个几何体的体积为( )
某几何体的三视图如图所示,其俯视图是边长为1的正三角形,侧视图是菱形,则这个几何体的体积为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
| A. | 130 | B. | 132 | C. | 134 | D. | 136 |