题目内容
过抛物线y2=2px(p>0)的焦点作倾斜角为30°的直线l与抛物线交于P、Q两点,分别过P、Q两点作PP1,QQ1垂直于抛物线的准线于P1、Q1,若|PQ|=2,则四边形PP1Q1Q的面积是( )
A、
| ||
| B、2 | ||
| C、3 | ||
| D、1 |
考点:直线与圆锥曲线的关系,抛物线的简单性质
专题:数形结合,转化思想,圆锥曲线的定义、性质与方程
分析:分析:这是一个抛物线的焦点弦问题,所以要尽可能的利用抛物线的定义、性质结合图象将问题合理转化后求解.
解答:
解:如图所示:由已知得|PP1|+|QQ1|=|PQ|=2,
所以直角梯形PP1QQ1 的面积S=
(|PP1|+|QQ1|)|P1Q1|=
|PQ||P1Q1|=|P1Q1|,
又因为∠QPP1=30°,所以在直角梯形PP1QQ1中,|P1Q1|=|PQ|sin∠QPP1=2sin30°=1.
所求四边形PP1Q1Q的面积为1.
故选D

所以直角梯形PP1QQ1 的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
又因为∠QPP1=30°,所以在直角梯形PP1QQ1中,|P1Q1|=|PQ|sin∠QPP1=2sin30°=1.
所求四边形PP1Q1Q的面积为1.
故选D

点评:抛物线的焦点弦问题常从定义出发,将抛物线上的点到焦点的距离和到准线的距离相互转换,将所求的问题转化为我们所熟知的问题解决;同时要强化解析几何问题做题先画图的思想意识,充分利用数形结合的思想解题.
另外,本题也可以借助于方程的思想求解,即先利用直线与抛物线方程联立消元,利用韦达定理、弦长公式求出p的值,再将所求的面积用P、Q的坐标表示,最后利用韦达定理采用“设而不求”的方法将面积表示并求出来.
另外,本题也可以借助于方程的思想求解,即先利用直线与抛物线方程联立消元,利用韦达定理、弦长公式求出p的值,再将所求的面积用P、Q的坐标表示,最后利用韦达定理采用“设而不求”的方法将面积表示并求出来.

练习册系列答案
相关题目
已知全集U=R,集合A={x|log3x≤0},B={3x≥
},A∩B=( )
| 1 |
| 3 |
| A、[-1,1] |
| B、(0,3] |
| C、(0,1] |
| D、[-1,3] |
已知复数z=
,则复数z的共轭复数在复平面内对应的点在( )
| 2+i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设x,y满足不等式组
,若z=ax+y的最大值为2a+6,最小值为2a-2,则实数a的取值范围是( )
|
| A、(-1,1) |
| B、[-1,1] |
| C、[-1,2) |
| D、[-1,2] |
设i是虚数单位,
是复数z=
+
i的共轭复数,则z2•
=( )
. |
| z |
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
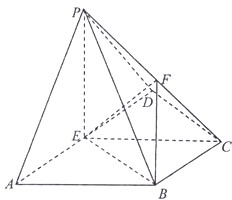 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.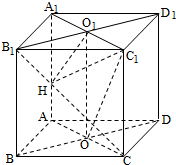 如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.