题目内容
已知双曲线
-
=1(a>0,b>0),过右焦点F的直线与双曲线交于A、B两点,且AB的中点为D(4,2),双曲线的离心率为
,则双曲线两焦点的距离等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、7 | ||
B、
| ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:双曲线的离心率为
,可得
=
,利用点差法,结合斜率公式,即可求出双曲线两焦点的距离.
| 3 |
| b |
| a |
| 2 |
解答:
解:∵双曲线的离心率为
,
∴
=
,∴
=
,
设A(x1,y1),B(x2,y2),则
由点差法可得
=
•
=4
∵
=
,
∴
=4,
∴c=
,
∴2c=7,
故选:A.
| 3 |
∴
1+(
|
| 3 |
| b |
| a |
| 2 |
设A(x1,y1),B(x2,y2),则
由点差法可得
| y1-y2 |
| x1-x2 |
| b2 |
| a2 |
| x1+x2 |
| y1+y2 |
∵
| y1-y2 |
| x1-x2 |
| 2-0 |
| 4-c |
∴
| 2-0 |
| 4-c |
∴c=
| 7 |
| 2 |
∴2c=7,
故选:A.
点评:本题考查双曲线两焦点的距离,考查点差法,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
数列{an}的前n项和为Sn,且Sn=2Sn+1+an2,a2=-1,则数列{an}的首项为( )
| A、1或-2 | B、±1 |
| C、±2 | D、-1或2 |
若执行如图所示的框图,输入x1=1,x2=2,x3=4,x4=8,则输出的数等于( )
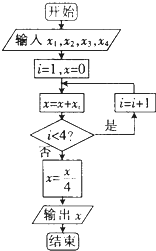

A、
| ||
B、
| ||
C、
| ||
| D、3 |
函数y=-x2的单调区间为( )
| A、(-∞,0)为减区间 |
| B、(0,+∞)为增区间 |
| C、(-∞,+∞) |
| D、(-∞,0)为增区间,(0,+∞)为减区间 |
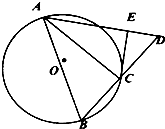 如图,AB是圆O的弦,点C在圆O上,延长BC到D,使BC=CD,AB=AD.
如图,AB是圆O的弦,点C在圆O上,延长BC到D,使BC=CD,AB=AD. 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于