题目内容
已知数列{an}的前n项和Sn=n2(n∈N*),数列{bn}是各项均为正数的等比数列,b1=1,b5=16.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=
,求证:数列{cn}的前n项和Tn≥1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=
| an |
| bn |
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)n≥2时,an=Sn-Sn-1=2n-1,n=1时,a1=S1=1,满足上式,由此求出an=2n-1(n∈N*).由b5=b1q4=q4=16,bn>0,求出bn=2n-1(n∈N*).
(2)由cn=
=
,利用错位相减法求出Tn=6-
,n∈N*.由此能证明Tn≥1.
(2)由cn=
| an |
| bn |
| 2n-1 |
| 2n-1 |
| 2n+3 |
| 2n+1 |
解答:
(1)解:n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
n=1时,a1=S1=1,满足上式,
∴an=2n-1(n∈N*).
∵b5=b1q4=q4=16,bn>0,∴q=2,
∵b1=1,∴bn=2×2n-1=2n-1(n∈N*).
(2)证明:∵cn=
=
,
∴Tn=
+
+
+…+
.①
Tn=
+
+
+
+…+
,②
①-②,得:
Tn=2+2•(
+
+…+
)-
=2+2×
-
=3-
,
∴Tn=6-
,n∈N*.
∵Tn+1-Tn=[6-
]-(6-
)
=-
+
=
=
>0.
又T1=1,∴Tn≥1.
n=1时,a1=S1=1,满足上式,
∴an=2n-1(n∈N*).
∵b5=b1q4=q4=16,bn>0,∴q=2,
∵b1=1,∴bn=2×2n-1=2n-1(n∈N*).
(2)证明:∵cn=
| an |
| bn |
| 2n-1 |
| 2n-1 |
∴Tn=
| 1 |
| 20 |
| 3 |
| 2 |
| 5 |
| 22 |
| 2n-1 |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 22 |
| 5 |
| 23 |
| 7 |
| 24 |
| 2n-1 |
| 2n |
①-②,得:
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
| 2n-1 |
| 2n |
=2+2×
| ||||
1-
|
| 2n-1 |
| 2n |
=3-
| 2n+3 |
| 2n |
∴Tn=6-
| 2n+3 |
| 2n+1 |
∵Tn+1-Tn=[6-
| 2(n+1)+3 |
| 2n |
| 2n+3 |
| 2n-1 |
=-
| 2(n+1)+3 |
| 2n |
| 2n+3 |
| 2n-1 |
=
| -(2n+5)+4n+6 |
| 2n |
=
| 2n+1 |
| 2n |
又T1=1,∴Tn≥1.
点评:本题考查数列的通项公式的求法,考查数列的前n项和大于等于1的证明,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.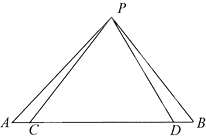 如图,C,D两点在△PAB的边AB上,AC=BD,若∠CPD=90°,且PA2+PB2=10,则2AB+CD的最大值为
如图,C,D两点在△PAB的边AB上,AC=BD,若∠CPD=90°,且PA2+PB2=10,则2AB+CD的最大值为