题目内容
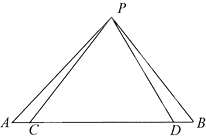 如图,C,D两点在△PAB的边AB上,AC=BD,若∠CPD=90°,且PA2+PB2=10,则2AB+CD的最大值为
如图,C,D两点在△PAB的边AB上,AC=BD,若∠CPD=90°,且PA2+PB2=10,则2AB+CD的最大值为考点:向量在几何中的应用,向量加减混合运算及其几何意义
专题:平面向量及应用
分析:如图所示,以CD的中点为坐标原点,AB所在直线为x轴建立直角坐标系.不妨设C(-a,0),D(a,0),B(a+b,0),A(-a-b,0),P(x,y).
由∠CPD=90°,利用圆的方程可得x2+y2=a2.由PA2+PB2=10,利用两点之间的距离公式可得(x+a+b)2+y2+(x-a-b)2+y2=10,
化为(a+b)2+a2=5.再利用数量积的性质可得2AB+CD=2(2a+2b)+2a=4(a+b)+2a≤
•
即可得出.
由∠CPD=90°,利用圆的方程可得x2+y2=a2.由PA2+PB2=10,利用两点之间的距离公式可得(x+a+b)2+y2+(x-a-b)2+y2=10,
化为(a+b)2+a2=5.再利用数量积的性质可得2AB+CD=2(2a+2b)+2a=4(a+b)+2a≤
| (a+b)2+a2 |
| 42+22 |
解答:
解:如图所示,以CD的中点为坐标原点,AB所在直线为x轴建立直角坐标系.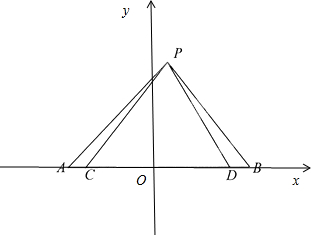
不妨设C(-a,0),D(a,0),B(a+b,0),A(-a-b,0),P(x,y).
∵∠CPD=90°,∴x2+y2=a2.
∵PA2+PB2=10,∴(x+a+b)2+y2+(x-a-b)2+y2=10,
化为(a+b)2+a2=5.
∴2AB+CD=2(2a+2b)+2a=4(a+b)+2a≤
•
=10,
当且仅当向量(4,2)与向量(a+b,a)共线时取等号.
∴2AB+CD的最大值为10.
故答案为:10.

不妨设C(-a,0),D(a,0),B(a+b,0),A(-a-b,0),P(x,y).
∵∠CPD=90°,∴x2+y2=a2.
∵PA2+PB2=10,∴(x+a+b)2+y2+(x-a-b)2+y2=10,
化为(a+b)2+a2=5.
∴2AB+CD=2(2a+2b)+2a=4(a+b)+2a≤
| (a+b)2+a2 |
| 42+22 |
当且仅当向量(4,2)与向量(a+b,a)共线时取等号.
∴2AB+CD的最大值为10.
故答案为:10.
点评:本题考查了两点之间的距离公式、数量积的性质、圆的方程等基础知识与基本技能方法,考查了数形结合的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
若平面向量
,
的夹角为60°,且|
|=2|
|,则( )
| a |
| b |
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设
,
是非零向量,则下列说法正确的是( )
| a |
| b |
A、若
| ||||||||||||
B、若
| ||||||||||||
C、若
| ||||||||||||
D、若存在实数λ,使
|
 如图,直线l1,l2交于点A,点B、C在直线l1,l2上,已知∠CAB=45°,AB=2,设
如图,直线l1,l2交于点A,点B、C在直线l1,l2上,已知∠CAB=45°,AB=2,设