题目内容

已知a+b=1，求证：a3+b3+3ab=1．
考点：二维形式的柯西不等式
专题：证明题,综合法
分析：由a+b=1，可得b=1-a，代入a3+b3+3ab，化简即可得出结论．
解答： 证明：∵a+b=1，∴b=1-a．
∴a3+b3+3ab=a3+（1-a）3+3a（1-a）=a3+1-3a+3a2-a3+3a-3a2=1
即a3+b3+3ab=1．
点评：本题考查不等式的证明，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知
m
=（sinx，
3
sinx），
n
=（sinx，cosx），设函数f（x）=
m
•
n

（1）求函数f（x）的解析式；
（2）求函数f（x）在区间[-
π
4
，
π
6
]上的最小值．
用二项式定理证明：
（1）2n+2•3n+5n-4（n∈N*）能被25整除；
（2）（
2
3
）n-1＜
2
n+1
（n∈N*，且n≥3）．
已知n∈N+，求证：2n＞1+2+3+…+n．
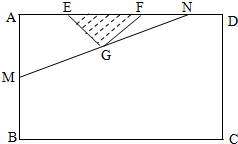某小区想利用一矩形空地ABCD建市民健身广场，设计时决定保留空地边上的一水塘（如图中阴影部分），水塘可近似看作一个等腰直角三角形，其中AD=60m，AB=40m，且△EFG中，∠EGF=90°，经测量得到AE=10m，EF=20m．为保证安全同时考虑美观，健身广场周围准备加设一个保护栏．设计时经过点G作一直线交AB，DF于M，N，从而得到五边形MBCDN的市民健身广场，设DN=x（m）．
（1）将五边形MBCDN的面积y表示为x的函数；
（2）当x为何值时，市民健身广场的面积最大？并求出最大面积．
已知数列{an}的前n项和Sn=n2（n∈N*），数列{bn}是各项均为正数的等比数列，b1=1，b5=16．
（1）求数列{an}和{bn}的通项公式；
（2）设cn=
an
bn
，求证：数列{cn}的前n项和Tn≥1．
已知
a
=（-cosx，sinx），
b
=（cosx，
3
cosx），f（x）=
a
•
b
，x∈[0，π]，则当f（x）取最大值时，求
a
，
b
的夹角．
已知二次函数f（x）=x2+ax+4，若f（x+1）是偶函数，则实数a的值为
 
．
已知f（x）的定义域为[-1，3]，则f（x2）的定义域为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网