题目内容
记关于x的不等式
<0的解集为P,不等式|x-1|<1的解集为Q.
(1)若a=3,求P;
(2)若a=-1,求P∪Q.
| x-a |
| x-1 |
(1)若a=3,求P;
(2)若a=-1,求P∪Q.
考点:其他不等式的解法,并集及其运算
专题:不等式的解法及应用
分析:(1)若a=3,由关于x的不等式可得
<0,故有(x-1)(x-3)<0,解此一元二次不等式求得P.
(2)若a=-1,由关于x的不等式可得
<0,即(x-1)(x+1)<0,求得 P,再解绝对值不等式求得Q,再根据两个集合的并集的定义求得P∪Q.
| x-3 |
| x-1 |
(2)若a=-1,由关于x的不等式可得
| x+1 |
| x-1 |
解答:
解:(1)若a=3,由关于x的不等式
<0可得
<0,故有(x-1)(x-3)<0,
解得 1<x<3,故P=(1,3).
(2)若a=-1,由关于x的不等式
<0可得
<0,即(x-1)(x+1)<0,
解得-1<x<1,故P=(-1,1).
由不等式|x-1|<1可得-1<x-1<1,解得 0<x<2,故Q=(0,2),
故P∪Q=(-1,2).
| x-a |
| x-1 |
| x-3 |
| x-1 |
解得 1<x<3,故P=(1,3).
(2)若a=-1,由关于x的不等式
| x-a |
| x-1 |
| x+1 |
| x-1 |
解得-1<x<1,故P=(-1,1).
由不等式|x-1|<1可得-1<x-1<1,解得 0<x<2,故Q=(0,2),
故P∪Q=(-1,2).
点评:本题主要考查分式不等式的解法,体现了等价转化的数学思想,属于中档题.

练习册系列答案
相关题目
不等x|x|<x的解集是( )
| A、{x|0<x<1} |
| B、{x|-1<x<1} |
| C、{x|0<x<1}或{x|x<-1}, |
| D、{x|-1<x<0,x>1} |
不等式x>
的解集是( )
| 1 |
| x |
| A、{x|x<1} |
| B、{x|x<-1或x>1} |
| C、{x|-1<x<1} |
| D、{x|-1<x<0或x>1} |
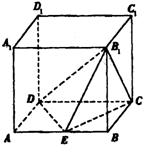 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点.设正方体的棱长为2a.
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点.设正方体的棱长为2a.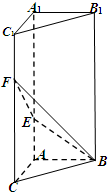 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,