Question

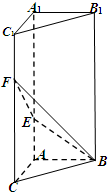如图，在直三棱柱ABC-A₁B₁C₁中，∠BAC=

π

2

，AB=AC=2，AA₁=6，点E、F分别在棱AA₁、CC₁上，且AE=C₁F=2．
（1）求四棱锥B-AEFC的体积；
（2）求△BEF所在半平面与△ABC所在半平面所成二面角θ的余弦值．

Answer 1

考点：二面角的平面角及求法,棱柱、棱锥、棱台的体积

专题：空间角

分析：（1）由已知条件可判出AB⊥面AA₁C₁C，求出直角梯形AEFC的面积，则四棱锥B-AEFC的体积可求；
（2）以A为坐标原点建立空间直角坐标系，求出平面ABC与平面BEF的法向量，利用平面法向量所成角的余弦值得△BEF所在半平面与△ABC所在半平面所成二面角θ的余弦值．

解答： 解：（1）因为三棱柱ABC-A₁B₁C₁为直三棱柱，所以A₁A⊥底面ABC，所以A₁A⊥AB，
又AB⊥AC，AC∩A₁A=A，所以AB⊥面AA₁C₁C，则AB为四棱锥B-AEFC的高．
在直角梯形AEFC中，因为AE=2，AC=2，CF=4，所以SAEFC=

1

2

(2+4)×2=6．
所以V_B-AEFC=

1

3

SAEFC•AB=

1

3

×6×2=4．
（2）以A为坐标原点，分别以AC，AB，AA₁所在直线为x，y，z建立如图所示的直角坐标系，

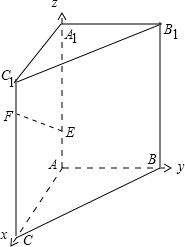
则A（0，0，0），B（0，2，0），E（0，0，2），F（2，0，4），

EF

=(2，0，2)，

EB

=(0，2，-2)
设平面BEF的法向量为

n

=(x，y，z)，则

n • EF =0 n • EB =0

，则

2x+2z=0 2y-2z=0

，取z=1，得x=-1，y=1．
所以

n

=(-1，1，1)．
平面ABC的一个法向量为

n

1=(0，0，1)，
则cosθ=

n • n 1

| n |•| n 1|

=

1

3

=

3

3

．
所以△BEF所在半平面与△ABC所在半平面所成二面角θ的余弦值为

3

3

．

点评：本题考查了椎体体积的求解方法，考查了利用空间向量求二面角的平面角，解答的关键是建立正确的空间坐标系，是中档题．