题目内容

不等x|x|＜x的解集是（　　）
A、{x|0＜x＜1}
B、{x|-1＜x＜1}
C、{x|0＜x＜1}或{x|x＜-1}，
D、{x|-1＜x＜0，x＞1}
考点：绝对值不等式
专题：不等式的解法及应用
分析：建议修改C为 {x|0＜x＜1，或 x＜-1}

原不等式即x（|x|-1）＜0，等价转化为①
x＞0
|x|-1＜0
，或 ②
x＜0
|x|-1＞0
．分别求得①、②的解集，
再取并集，即得所求．
解答： 解：不等x|x|＜x，即 x（|x|-1）＜0，∴①
x＞0
|x|-1＜0
，或 ②
x＜0
|x|-1＞0
．
解①可得 0＜x＜1，解②可得 x＜-1．
把①②的解集取并集，即得原不等式的解集为 {x|0＜x＜1}或{x|x＜-1}，
故选C．
点评：本题主要考查绝对值不等式的解法，体现了分类讨论和等价转化的数学思想，属于中档题．
练习册系列答案
相关题目
极坐标方程p=cosθ化为直角坐标方程是
 
．
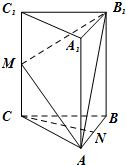如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=BC=2，AB=2
2
，CC1=4，M是棱CC1上一点．
（Ⅰ）求证：BC⊥AM；
（Ⅱ）若M，N分别为CC1，AB的中点，求证：CN∥平面AB1M．
记关于x的不等式
x-a
x-1
＜0的解集为P，不等式|x-1|＜1的解集为Q．
（1）若a=3，求P；
（2）若a=-1，求P∪Q．
在直角梯形ABCD中∠ABC=∠DAB=90°，∠CAB=30°，BC=1，AD=CD，把△DAC沿对角线AC折起后如图所示（点D记为点P），点P在平面ABC上的正投影E落在线段AB上，连接PB．若F是AC的中点，连接PF，EF．
（1）求证：AC⊥平面PEF．
（2）求直线PC与平面PAB所成的角的大小．
函数f（x）=xsinx-1在(-
π
2
，
π
2
)上的零点个数为（　　）
A、5B、4C、3D、2
已知f(x)=atanx+b
3x
+1（a，b为实数），且f（lglog310）=5，则f（lglg3）=
 
．
已知向量
a
=（-1，cosωx+
3
sinωx），
b
=（f（x），cosωx），其中ω＞0，且
a
⊥
b
，又f（x）的图象两相邻对称轴的距离为
3
2
π．
（1）求ω的值；
（2）求函数f（x）在[0，2π]上的单调递减区间．
为了实现长沙经济区域一体化战略，湖南省政府计划对长沙市周边如图所示的A，B，C，D，E，F，G，H八个中小城市进行综合规划治理，第一期工程拟从这八个中小城市中选取3个城市，但要求没有任何两个城市相邻，则城市A被选中的概率为（　　）
A、
3
8
B、
5
28
C、
5
13
D、
1
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网