题目内容

17．设等差数列{an}的前n项和为Sn，已知a1+a2+a3=a4+a5，S5=60，则a10=（　　）
A．16B．20C．24D．26

分析 利用等差数列有通项公式、前n项和公式列出方程组，求出首项及公差，由此能求出结果．

解答 解：∵等差数列{an}的前n项和为Sn，
a1+a2+a3=a4+a5，S5=60，
∴$\left\{\begin{array}{l}{3{a}_{1}+3d=2{a}_{1}+7d}\\{5{a}_{1}+\frac{5×4}{2}d=60}\end{array}\right.$，
解得a1=8，d=2，
a10=8+9×2=26．
故选：D．

点评 本题考查等差数列的第10项的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案
相关题目
14．已知向量$\overrightarrow a=（{1，x}），\overrightarrow b=（{1，x-1}）$，若$（{\overrightarrow a-2\overrightarrow b}）⊥\overrightarrow a$，则$|{\overrightarrow a-2\overrightarrow b}|$=$\sqrt{2}$．
8．已知tanα=2，则cos2α-sinαcosα=-1．
5．已知向量$\overrightarrow{O{P}_{1}}$，$\overrightarrow{O{P}_{2}}$，$\overrightarrow{O{P}_{3}}$，满足$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$+$\overrightarrow{O{P}_{3}}$=0，且|$\overrightarrow{O{P}_{1}}$|=|$\overrightarrow{O{P}_{2}}$|=|$\overrightarrow{O{P}_{3}}$|=1，则|$\overrightarrow{{P}_{1}{P}_{2}}$|=$\sqrt{3}$．
12．若二次函数 y=x2+mx+1有两个不同的零点，则m的取值范围是（-∞，-2）∪（2，+∞）．
2．已知函数f（x）=2sin2（x+$\frac{π}{4}$）-$\sqrt{3}$cos2x-1，x∈[$\frac{π}{4}$，$\frac{π}{2}$]．
（1）求f（x）的最小值；
（2）若f（x）=$\frac{3}{2}$，求f（x-$\frac{π}{6}$）的值．
9．用1，2，3，4组成无重复数字的三位数，这些数能被2整除的概率是$\frac{1}{2}$．
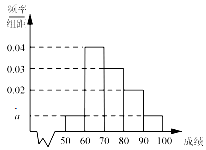6．某校100名学生期中考试物理成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求图中物理成绩的众数及a的值；
（2）根据频率分布直方图，估计这100名学生物理成绩的平均分和中位数（中位数要求精确到小数点后一位）．
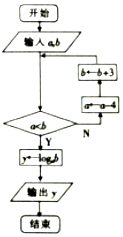7．如图是一个算法的流程图，当输入a=10，b=2的时，输出的y值为3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网