题目内容
9.用1,2,3,4组成无重复数字的三位数,这些数能被2整除的概率是$\frac{1}{2}$.分析 求出无重复数字的三位数的个数是6,其中这些数被4整除的有2个,由此求得这些数被4整除的概率
解答 解:用1,2、3、4组成无重复数字的三位数,共有4×3×2=24个,
其中这些数被2整除的有${C}_{2}^{1}$•3•2=12个,
故这些数被2整除的概率是$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 本题考查古典概型及其概率计算公式的应用,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
20.执行如图所示的程序框图,若输入n的值为8,则输出S的值为( )


| A. | 4 | B. | 8 | C. | 10 | D. | 12 |
17.设等差数列{an}的前n项和为Sn,已知a1+a2+a3=a4+a5,S5=60,则a10=( )
| A. | 16 | B. | 20 | C. | 24 | D. | 26 |
1. 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
(1)从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
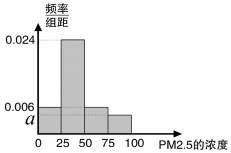
(2)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.
①求图中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表| 组别 | PM2.5浓度 (微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 3 | 0.15 |
| 第二组 | (25,50] | 12 | 0.6 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
(2)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.
①求图中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.