题目内容
直线L过抛物线C:y2=2px(p>0)的焦点F且与C相交于A、B两点,且AB的中点M的坐标为(3,2),则抛物线C的方程为( )
| A、y2=2x或y2=4x |
| B、y2=4x或y2=8x |
| C、y2=6x或y2=8x |
| D、y2=2x或y2=8x |
考点:抛物线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:先利用点差法,求出AB的斜率,可得直线AB的方程为y=
(x-
),代入y2=2px,利用中点坐标公式,即可得出抛物线C的方程.
| p |
| 2 |
| p |
| 2 |
解答:
解:抛物线y2=2px的焦点为F(
,0)
设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,
两式相减可得:y12-y22=2p(x1-x2),
∴kAB=
=
,
直线AB的方程为y=
(x-
),代入y2=2px,可得4px2-(4p2+32)x+p3=0
可得x1+x2=
=6,解之得p=2或4,
∴物线C的方程为y2=4x或y2=8x.
故选:B.
| p |
| 2 |
设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,
两式相减可得:y12-y22=2p(x1-x2),
∴kAB=
| 2p |
| y1+y2 |
| p |
| 2 |
直线AB的方程为y=
| p |
| 2 |
| p |
| 2 |
可得x1+x2=
| p2+8 |
| p |
∴物线C的方程为y2=4x或y2=8x.
故选:B.
点评:本题考查抛物线C的方程,考查点差法,考查学生的计算能力,比较基础.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
下列各组命题中,满足“p或q为真”,且“非p为真”的是( )
| A、p:0=∅;q:0∈∅ | ||||
| B、p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数 | ||||
C、p:a+b≥2
| ||||
D、p:圆(x-1)2+(y-2)2=1的面积被直线|x|=1平分;q:椭圆
|
函数y=-
的大致图象是( )
| 1 |
| x+1 |
A、 |
B、 |
C、 |
D、 |
”a<0”是”函数f(x)=|x(x-2a)|在区间(0,+∞)上单调递增”的( )
| A、必要不充分条件 |
| B、充要条件 |
| C、既不充分也不必要条件 |
| D、充分不必要条件 |
下列式子一定成立的是( )
| A、P(B|A)=P(A|B) |
| B、P(AB)=P(A|B)•P(B)=P(B|A)•P(A) |
| C、0<P(A|B)<1 |
| D、P(A∩B|A)=P(B) |
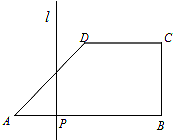 在直角梯形ABCD中,AB∥DC,AB⊥BC,且AB=4,BC=CD=2,点P为线段AB上的一动点,过点P作直线l⊥AB,令AP=x,记梯形位于直线l左侧部分的面积S=f(x).
在直角梯形ABCD中,AB∥DC,AB⊥BC,且AB=4,BC=CD=2,点P为线段AB上的一动点,过点P作直线l⊥AB,令AP=x,记梯形位于直线l左侧部分的面积S=f(x).